Рассмотрим произвольное вероятностное пространство ![]() и два события А и В. Будем считать, что
и два события А и В. Будем считать, что ![]() .
.
Что можно сказать о вероятности события В, если известно, что произошло событие А?
Тот факт, что событие А произошло, несет некоторую дополнительную информацию о пространстве элементарных исходов, что, возможно, изменяет вероятность появления В.
По определению вероятность события В, найденная в предположении, что произошло некоторое событие А, называется условной вероятностью события В (обозначается ![]() ).
).
Если событие А произошло, то некоторые из элементарных исходов становятся невозможными: ![]() . И мы можем рассматривать новое усеченное пространство элементарных исходов, из которых невозможные исходы исключены, т.е.
. И мы можем рассматривать новое усеченное пространство элементарных исходов, из которых невозможные исходы исключены, т.е. ![]() .
.
Например, при классическом определении вероятности условную вероятность можно подсчитать в этом новом пространстве элементарных исходов следующим образом:
![]() ;
; 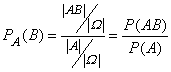 .
.
Условной вероятностью события В называется число, равное отношению вероятности совместного появления событий к вероятности события А:
![]() . (1.8)
. (1.8)
Условная вероятность, определенная таким образом, удовлетворяет всем аксиомам (1.1) – (1.3) в определении вероятности.
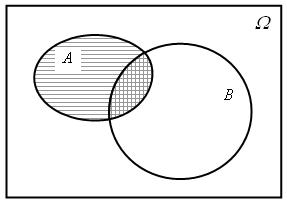
Рис. 1.10. Диаграмма Эйлера-Венна
Действительно:
1) так как ![]() (рис. 1.10) (
(рис. 1.10) (![]() по условию), то
по условию), то
![]() ,
,
следовательно, справедлива аксиома (1.1);
2) ![]() ,
,
следовательно, справедлива аксиома (1.2);
3) если В и С несовместные события, т.е. ![]() , то события АВ и АС тоже несовместны
, то события АВ и АС тоже несовместны
![]() ,
,
тогда
![]() ,
,
следовательно, справедлива аксиома (1.3).
Пример 1
Студент идет на экзамен, зная первые пять билетов из первого десятка и пять последних билетов из третьего десятка. Общее количество билетов 30. Ему достается билет из первого десятка. Найти вероятность того, что билет знаком студенту.
Решение
Пусть событие А – билет извлечен из первого десятка, событие В – билет знаком студенту. Тогда
![]() ,
, ![]() ,
,![]() .
.
![]() ,
, ![]()
![]() .
.
Если использовать формулу (1.8), то получится:
![]() .
.
Равенство (1.8) можно представить в следующем виде:
![]() . (1.9)
. (1.9)
Это теорема умножения. Её можно представить в следующем виде:
![]() .
.
Эти формулы легко обобщаются на случай n сомножителей:
![]() (1.10)
(1.10)
Пример 2
Студент идет на экзамен, выучив 15 из 30 вопросов. Ему предлагают билет из трех вопросов. Найти вероятность того, что студент знает все три вопроса.
Решение
Пусть
![]() ,
,
где ![]() – i-й вопрос знаком студенту.
– i-й вопрос знаком студенту.
Тогда
![]() ;
;
![]() .
.
Событие В – хотя бы один вопрос знаком студенту, тогда
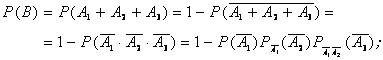
![]() .
.
В общем случае имеем:
![]() .
.
Если вероятность появления одного из событий не зависит от того, произошло ли другое, то эти события называются независимыми.
Для независимых событий
![]() .
.
События ![]() называются независимыми в совокупности, если для любого набора индексов
называются независимыми в совокупности, если для любого набора индексов ![]() справедливы равенства:
справедливы равенства:
![]()
или
![]() .
.
Из независимости в совокупности следует попарная независимость, но, вообще говоря, не наоборот, т.е. попарная независимость не является достаточным условием независимости в совокупности.
Пример 3
Пусть имеется урна с 4 шарами, в которой: 1 – белый шар, 1 – черный, 1 – красный, 1 – раскрашен в три цвета.
Решение
Событие А – извлеченный наудачу шар содержит в окраске белый цвет, событие В – извлеченный наудачу шар содержит в окраске черный цвет, событие С – извлеченный наудачу шар содержит в окраске красный цвет. Тогда
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ,
,
т.е. события попарно независимы, но
![]() ,
,
или, например,
![]() .
.
Следовательно, события ![]() зависимы в совокупности.
зависимы в совокупности.