По формуле Бернулли ![]() , где
, где ![]() , найдем отношение:
, найдем отношение:
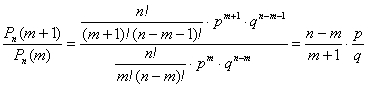 .
.
Если ![]() , то
, то
![]()
![]() ;
;
![]()
![]() .
.
Значит, существует ![]() – наивероятнейшее число появлений события А.
– наивероятнейшее число появлений события А.
Рассмотрим второе неравенство:
![]() ,
, ![]() .
.
1) Если ![]() – целое число, то пусть
– целое число, то пусть ![]() и тогда:
и тогда:
![]() .
.
Таким образом,
![]() ,
,
т.е. ![]() — два наивероятнейших числа появлений события А в испытаниях.
— два наивероятнейших числа появлений события А в испытаниях.
2) Если ![]() – нецелое число, то обозначим через
– нецелое число, то обозначим через ![]() – наименьшее целое число большее
– наименьшее целое число большее ![]() , т.е. в этом случае
, т.е. в этом случае ![]() определяется как решение неравенств:
определяется как решение неравенств:
![]()
или
![]() .
.