По формуле Бернулли (1.15) в том случае, когда число испытаний очень большое, а вероятность появления или непоявления события А мала, ничего посчитать практически невозможно. В этом случае перемножаются очень большие числа и очень маленькие и за счет ошибок округления возникают большие погрешности. В данной ситуации используются приближенные формулы.

Теорема 3 (Пуассона)

Если при  так, что , тогда

             (1.17)

Справедлива приближенная формула Пуассона

Пример 1

Пекарня выпекает булочки с изюмом, среднее число изюминок в булочке равно 5. Что вероятнее: купить булочку с 4 или с 6 изюминками.

Решение

По формуле Пуассона (1.17) находим:

;                       ;

то есть

.

Теорема 4 (локальная теорема Лапласа)

Если при

,

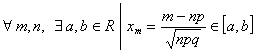то

,

 – локальная функция Лапласа.

При , справедлива локальная формула Муавра-Лапласа:

                   (1.18)

где.

Теорема 5 (интегральная теорема Лапласа)

При  

,

где  – интегральная функция Лапласа.

Если , то справедлива интегральная формула Лапласа

,                 (1.19)

где .

Пример 2

Вероятность появления события А в одном испытании равна p = 0,7. Найти вероятность того, что в 100 независимых испытаниях событие А произойдет от 60 до 90 раз.

Решение

Решим поставленную задачу приближенным способом с помощью интегральной теоремы Лапласа:

,

где .

Находим:

;

.

Таблица значений интегральной функции Лапласа Ф(x) для положительных x приведена в приложении 1. Причем функция Ф(x) – нечетная, т.е. .

Для всех значений x > 4 принимают .

В нашем случае:

;

.

Тогда вероятность равна:

.