Числа, которыми мы привыкли пользоваться, называются десятичными, а арифметика — десятичной системой счисления. Это потому, что каждое число можно составить из набора цифр содержащего 10 символов – цифр: 1, 2, 3, 4, 5, 6, 7, 8. 9, 0. Под системой счисления понимают совокупность способов и средств записи чисел.

Со временем десятичный набор стал главным, но не единственным. С помощью замены 10 на любое другое число можно получить другую систему и другую арифметику.

Информация в ЭВМ хранится в двоичном виде (двоичной системе счисления). Это система счисления, в которой 10 заменяют на 2. Данная система определяется следующим образом:

где  – это символ «0» или «1». Эта система самая простая из всех возможных, так как в ней любое число образуется с помощью двух цифр 0 и 1.

Двоичное число можно представить в виде десятичного и, наоборот, десятичное — в виде двоичного.

Пример 1

Перевести двоичное число в десятичное.

Дано число в двоичное системе счисления 110011. Запишем данное число в десятичной системе счисления.

Решение

.

Получили число в десятичной системе счисления, равное 51.

Пример 2

Перевести десятичное число в двоичное.

Рассмотрим перевод числа 569₁₀ в двоичную систему счисления.

Решение

Десятичное число 569 делится на 2, что дает нам частное 284 и остаток 1. Этот остаток становится значением младшего разряда двоичного числа и помещается в крайнюю правую позицию. Затем частное 284 делится на 2, остаток от деления записывается в двоичное число, как более старший разряд. Процедуру деления частного повторяем до тех пор, пока частное не станет равно 0 или 1:

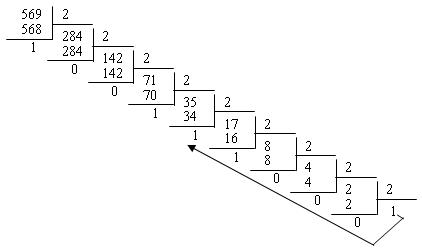
Запишем двоичное число из остатков частного от деления в направлении стрелки:

.

Ответ: 1000111001.