С применением методов математической статистики возможно не только оценить результаты и случайные погрешности химического анализа, но и провести сравнение данных. Часто возникает необходимость сравнения средних значений двух выборочных совокупностей. Это могут быть результаты химического анализа одного и того же объекта, полученные двумя разными равноточными методами, в двух разных лабораториях, различными химиками-аналитиками и т.д.
При сопоставлении двух средних значений ![]() и
и ![]() выборок с числом степеней свободы
выборок с числом степеней свободы ![]() и
и ![]() , прежде всего, сравнивают их дисперсии
, прежде всего, сравнивают их дисперсии ![]() и
и ![]() . Сравнение проводят при помощи F-распределения (распределения Фишера). Для этого рассчитывают экспериментальное значение F-критерия, равное отношению большей дисперсии к меньшей (при
. Сравнение проводят при помощи F-распределения (распределения Фишера). Для этого рассчитывают экспериментальное значение F-критерия, равное отношению большей дисперсии к меньшей (при ![]() ):
):
![]() .
.
Полученное значение Fэксп сравнивают с Fтабл для числа степеней свободы f1, f2 и заданной доверительной вероятности (табл. 9.4). Заметим, что в таблице число степеней свободы выборки с большей дисперсией приводится в горизонтальном ряду, выборки с меньшей дисперсией – в вертикальном ряду и что F(f1, f2) ¹ F(f2, f1).
Таблица 9.4
Значения критерия Фишера F при Рдов. = 0,95
|
f2 |
f1 |
|||||
|
2 |
3 |
4 |
5 |
6 |
¥ |
|
|
2 |
19,00 |
19,16 |
19,25 |
19,30 |
19,33 |
19,50 |
|
3 |
9,55 |
9,28 |
9,12 |
9,01 |
8,94 |
8,53 |
|
4 |
6,94 |
6,59 |
6,39 |
6,26 |
6,16 |
5,63 |
|
5 |
5,79 |
5,41 |
5,19 |
5,05 |
4,95 |
4,36 |
|
6 |
5,14 |
4,76 |
4,53 |
4,39 |
4,28 |
3,67 |
|
¥ |
3,00 |
2,60 |
2,37 |
2,21 |
2,10 |
1,00 |
Если Fэксп > Fтабл при заданной доверительной вероятности (обычно Рдов = 0,95 или 0,99), то расхождение между дисперсиями значимо и рассматриваемые выборочные совокупности отличаются по воспроизводимости. Объединять такие результаты нельзя.
Если Fэксп < Fтабл, то различие в воспроизводимости имеет случайный характер и обе дисперсии ![]() и
и ![]() являются приближенными оценками одной и той же обшей для обеих выборок дисперсии s2 генеральной совокупности.
являются приближенными оценками одной и той же обшей для обеих выборок дисперсии s2 генеральной совокупности.
Если расхождение между дисперсиями незначимо, то средние ![]() и
и ![]() двух выборочных совокупностей можно сравнивать. Цель этого сравнения – выяснить, есть ли статистически значимая разница в результатах химического анализа, полученных двумя различными методами, на двух разных приборах, разными аналитиками и т.д.
двух выборочных совокупностей можно сравнивать. Цель этого сравнения – выяснить, есть ли статистически значимая разница в результатах химического анализа, полученных двумя различными методами, на двух разных приборах, разными аналитиками и т.д.
Для решения поставленной задачи используют t-распределение. Рассчитывают средневзвешенную дисперсию (s2) и экспериментальное значение t-критерия:
![]() ,
, 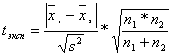 .
.
Сравнивают tэксп с tтабл при ![]() и доверительной вероятности Рдов = 0.95 или 0,99 (см. табл. 9.3).
и доверительной вероятности Рдов = 0.95 или 0,99 (см. табл. 9.3).
Если tэксп > tтабл, то расхождение между ![]() и
и ![]() значимо. Выборки не принадлежат одной генеральной совокупности, поэтому усреднять их результаты нельзя. Можно предположить наличие систематической погрешности в одной или обеих выборках.
значимо. Выборки не принадлежат одной генеральной совокупности, поэтому усреднять их результаты нельзя. Можно предположить наличие систематической погрешности в одной или обеих выборках.
Если tэксп < tтабл, то все данные можно рассматривать как единую выборочную совокупность с числом определений n = (n1 + n2). Результаты объединяют, рассчитывают для них ![]() , s и доверительный интервал.
, s и доверительный интервал.