Свойства основной задачи линейного программирования связаны со свойствами выпуклых множеств.

Система линейных неравенств с двумя неизвестными имеет вид:

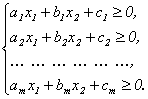                                                                                                         (2.7)

Для решения данной системы неравенств необходимо рассмотреть (истолковать) геометрический смысл каждого линейного неравенства, входящего в систему. Рассмотрим первое линейное неравенство:

                                                                                                    (2.8)

Истолковывая  х₁  и  х₂  как координаты точки на плоскости, естественно поставить вопрос: какую область на плоскости образуют точки, координаты которых удовлетворяют данному неравенству, или, выражаясь короче, какую область на плоскости определяет неравенство (2.8).

Если неравенство (2.8) обратить в равенство, то получим уравнение вида:

которое представляет собой прямую, например,  L.  В прямоугольной системе координат эту прямую можно графически построить следующим образом. Находят точки пересечения прямой с осями  х₁  и  х₂,  для чего поочередно приравнивают нулю  х₁  и  х_2.  Так, при  х₂ = 0  имеем     откуда  х₁ =  – (с₁ / а₁).  При  х₁ = 0  имеем    откуда  х₂ = – (с₁ / b₁).

Как видно из рисунка  2.1, прямая L разбивает плоскость, образуемую осями  х₁  и  х₂, на две полуплоскости (на рисунке числа  а₁, b₁, c₁ > 0), в одной из них выполняется условие

в другой

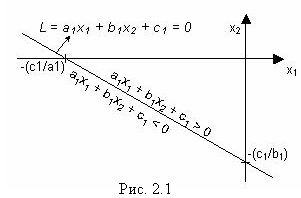
Прямую  L  мы считаем принадлежащей каждой из указанных полуплоскостей.

Практически, для того чтобы узнать,  какая  из  двух полуплоскостей соответствует неравенству (2.8), поступают следующим образом. Берут  произвольную точку координатной плоскости, не лежащую на прямой  L,  например точку (0; 0), подставляют ее в неравенство (2.8) Если в результате получаем неравенство  , значит исходное неравенство (2.8) определяет полуплоскость, лежащую над прямой  L. В противном случае, неравенство (2.8) определяет нижнюю полуплоскость, т.е. полу-плоскость, лежащую под прямой  L.