Так как любое предприятие функционирует в организационно-деловой среде, оперативно решая сложные повседневные проблемы в соответствии с поставленными целями и возникающими ситуациями, связанными с бесперебойным обеспечением ресурсами производственного процесса, то задачи, присущие динамике оперативного управления производством, решаются обычно на основе математических моделей, аналогичных рассматриваемым ранее для целей оптимального планирования.

Кроме нахождения оптимального решения должно быть обеспечено получение дополнительной информации о возможных изменениях решения при изменении параметров системы. Эту часть исследования обычно называют анализом модели на чувствительность.

Анализ устойчивости деятельности предприятия связан с изучением степени влияния динамики изменения показателей условий среды на результаты хозяйственной деятельности.

Так, после того как получено оптимальное решение по исходным статическим данным, проводится анализ моделей на чувствительность изменения оптимального решения к возможным изменениям внешних условий, т.е. динамики реальной жизни. Безусловный интерес представляют вопросы оценки влияния изменения спроса, запасов сырья, а также оптовых или розничных цен на оптимальное решение. В таком случае рассматривается по частям некоторая совокупность линейных оптимизационных моделей, что и придает модели динамичность, позволяющую проанализировать в совокупности влияние возможных изменений исходных условий на полученное оптимальное решение. Таким образом, проводится исследование хозяйственной деятельности на моделях, динамические характеристики которых отображают природу реальных процессов жизни, поскольку полученное статическое решение может устареть и быть непригодным для реализации.

Взаимосвязь экономических показателей рассматриваемой задачи можно представить в виде следующего выражения:

Доход = F (ресурсы, спрос, цены, инвестиции).

Перейдем к последовательному анализу влияния факторов на критерий целевой функции дохода. Но прежде, чем перейти к примерам, рассмотрим еще одну теорему, выводы которой будут использованы в дальнейшем.

Теорема (теорема об оценках)

Значения переменных y_i* в оптимальном решении двойственной задачи представляют собой оценки влияния свободных членов b_i системы ограничений-неравенств прямой задачи на величину ∆F*:

.

Другими словами, теорема о двойственных оценках позволяет определить приращение целевой функции при малых изменениях свободных членов системы ограничений. Таким образом, двойственная переменная оценивает влияние изменения каждого вида ресурса на целевую функцию (в связи с этим двойственные переменные часто называют двойственными оценками)

Решая ЗЛП симплексным методом, мы одновременно решаем двойственную ЗЛП. Значения переменных двойственной задачи y_i  в оптимальном плане называют, как уже отмечалось, двойственными оценками. Двойственные оценки определяют дефицитность используемых ресурсов. Величина двойственной оценки показывает, на

сколько изменится максимальное значение целевой функции прямой задачи при увеличении количества соответствующего ресурса на единицу.

Экономико-математический анализ решений осуществляется в двух основных направлениях:

ü в виде вариантных расчетов по моделям с сопоставлением различных вариантов плана;

ü в виде анализа каждого из полученных решений с помощью двойственных оценок.

Вариантные расчеты могут осуществляться при неизменной структуре самой модели (постоянном составе неизвестных, способов производства, ограничений задачи и одинаковом критерии оптимизации), но с изменением численных значений конкретных показателей модели. Вариантные расчеты могут проводиться также при варьировании элементов самой модели:

ü изменении критерия оптимизации;

ü добавлении новых ограничений на ресурсы или на способы производства их использования;

ü расширении множеств вариантов и т.д.

Одно из эффективных средств экономико-математического анализа – использование объективно обусловленных (двойственных) оценок оптимального плана. Такого рода анализ базируется на свойствах двойственных оценок. Экономическая интерпретация этих оценок может быть различной для разных задач.

Перейдем к рассмотрению конкретных экономических свойств оценок y_i оптимального плана (мы уже касались этого вопроса при изучении симплексного метода). Сначала перечислим эти свойства: 

1) оценки как мера дефицитности ресурсов и продукции;

2) оценки как мера влияния ограничений на функционал;

3) оценки как инструмент определения эффективности отдельных вариантов;

4) оценки как инструмент балансирования суммарных затрат и результатов,

а затем проиллюстрируем их конкретными примерами.

Пример. 2.35

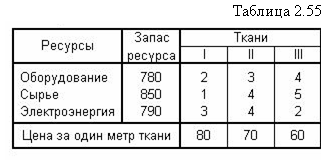(Задача о планировании выпуска тканей). Пусть некоторая фабрика выпускает три вида тканей, причем суточное плановое задание составляет не менее 90 м тканей первого вида, 70 м – второго и 60 м – третьего. Суточные ресурсы и их расход на один метр ткани, а также цена за один метр ткани представлены в таблице 2.55.

Необходимо определить, сколько метров ткани каждого вида следует выпустить, чтобы общая стоимость выпускаемой продукции была максимальной.