Определение. Число вида z = х + iy, где х, ![]() , a i – так называемая мнимая единица, называется комплексным числом. Мнимая единица определяется равенством:
, a i – так называемая мнимая единица, называется комплексным числом. Мнимая единица определяется равенством:
![]() (2.1)
(2.1)
Действительные числа x и y называются соответственно действительной и мнимой частью комплексного числа z и обозначаются:
x = Rez; y = Imz (2.2)
Множество комплексных чисел обозначают буквой С.
Например, ![]() – комплексное число, где Rez = 5 – действительная часть; Imz = 8 – мнимая часть.
– комплексное число, где Rez = 5 – действительная часть; Imz = 8 – мнимая часть.
Определение. Два комплексных числа считают равными тогда и только тогда, когда у них равны соответственно действительные и мнимые части. В частности, комплексное число z = х + iy равно нулю тогда и только тогда, когда х =0 и у =0 .
Определение. Числа z = х + iy и z = х – iy называются (комплексно) сопряженными.
 Пример 1
Пример 1
Записать сопряженное число для ![]() .
.
Решение
Сопряженное число: ![]() .
.
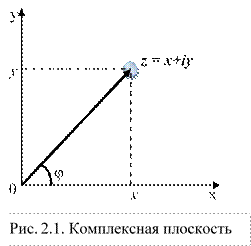
Выбираем на плоскости систему декартовых координат xОy (рис. 2.1) , тогда каждому z = х + iy будет соответствовать вектор ![]() плоскости, начало которого совпадает с началом координат, и, наоборот, каждому вектору
плоскости, начало которого совпадает с началом координат, и, наоборот, каждому вектору ![]() плоскости xОy будет отвечать определённое комплексное число z = х + iy (последнее следует из основной формулы векторного исчисления), где x и y – компоненты (координаты)
плоскости xОy будет отвечать определённое комплексное число z = х + iy (последнее следует из основной формулы векторного исчисления), где x и y – компоненты (координаты) ![]() .
.
Таким образом, между множеством C и множеством векторов (и точек!) плоскости xOy устанавливается взаимно однозначное соответствие.
Определения. Плоскость xОy называется плоскостью комплексных чисел (или просто комплексной плоскостью), будем её обозначать Z. Ось Ox – действительная ось; ось Oy – мнимая ось.
Поскольку ![]() – вектор, то он имеет длину и характеризуется направлением. Длину вектора
– вектор, то он имеет длину и характеризуется направлением. Длину вектора ![]() называют модулем комплексного числа z = х + iy, а величину угла наклона вектора
называют модулем комплексного числа z = х + iy, а величину угла наклона вектора ![]() по отношению к оси Ox – аргументом z. Их обозначают символами:
по отношению к оси Ox – аргументом z. Их обозначают символами:
![]() и
и ![]() . (2.3)
. (2.3)
Модуль комплексного числа есть однозначная функция:
![]() . (*)
. (*)
Из рисунка 2.1 видно, что:
![]() ,
, ![]() . (2.4)
. (2.4)
Аргумент ![]() есть функция многозначная. Все значения аргумента
есть функция многозначная. Все значения аргумента ![]() удовлетворяют соотношению:
удовлетворяют соотношению:
![]() (2.5)
(2.5)
При ![]() аргумент не определен. Из множества значений
аргумент не определен. Из множества значений ![]() (z
(z![]() 0) выделяют одно, лежащее в интервале
0) выделяют одно, лежащее в интервале ![]() , которое обозначают argz и называют главным значением аргумента:
, которое обозначают argz и называют главным значением аргумента:
![]() (2.6)
(2.6)
Очевидно, что
![]() (2.7)
(2.7)
Из формул (2.5) и (2.6) следует:
![]() (2.8)
(2.8)
 Пример 2
Пример 2
Дано комплексное число ![]() .
.
Необходимо: найти модуль комплексного числа, изобразить число на комплексной плоскости, найти главное значение аргумента комплексного числа.
Решение
Используем формулу (*) и находим модуль комплексного числа:
![]()
Изобразим число на комплексной плоскости (рис. 2.2).
Определим главное значение аргумента комплексного числа ![]() , используя формулу (2.8), так как
, используя формулу (2.8), так как ![]()
![]() т.е.
т.е. ![]() , то
, то
![]()