Рассмотрение метода хорд позволяет предположить, что итерации станут приближаться к корню ещё быстрее, если мы будем выбирать касательную вместо секущей не только на первом, а на каждом шаге. Ясно, что тогда формула итераций будет иметь вид:
![]() (3.4)
(3.4)
Этот метод называется методом касательных, или методом Ньютона. Действительно, сходимость метода Ньютона выше, чем общего метода итераций (скорость сходимости приближений в котором, напомним, та же, что у геометрической прогрессии со знаменателем ![]() при
при ![]() ).
).
Поскольку для метода Ньютона:
![]() (3.5)
(3.5)
то
![]() (3.6)
(3.6)
В точке ![]() получаем
получаем ![]() , так как
, так как ![]() .
.
Таким образом, при использовании метода касательных график ![]() пересекает прямую
пересекает прямую ![]() в точности по горизонтали, что приводит к очень быстрой сходимости итераций к
в точности по горизонтали, что приводит к очень быстрой сходимости итераций к ![]() . Оценка метода производится по формуле:
. Оценка метода производится по формуле:
![]() (3.7)
(3.7)
где c – некоторая постоянная (не зависящая от i).
Если начальное приближение ![]() взято достаточно близко от корня
взято достаточно близко от корня ![]() , то можно взять:
, то можно взять:
![]()
При оценке метода Ньютона с методом итераций получим:
![]() .
.
Постоянная ![]() заменяется в оценке метода Ньютона (3.7) на стремящуюся к 0 величину
заменяется в оценке метода Ньютона (3.7) на стремящуюся к 0 величину ![]() ; отсюда и высокая скорость сходимости.
; отсюда и высокая скорость сходимости.
Скорость сходимости итераций, которая задаётся формулой (3.7), называется квадратичной. Квадратичная скорость сходимости означает, примерно говоря, что число верных знаков в приближённом значении ![]() удваивается с каждой итерацией. Действительно, если:
удваивается с каждой итерацией. Действительно, если:
![]() , и
, и ![]() ,
,
то
![]() .
.
Это и означает, что число верных знаков при переходе к следующему приближению возросло с n до 2n, то есть удвоилось.
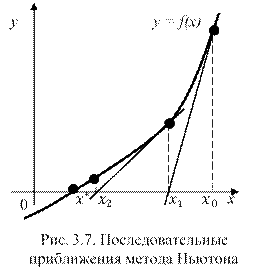
Геометрический смысл метода Ньютона состоит в том, что на каждом шаге мы строим касательную к графику y = f(x) (рис. 3.7) в точке очередного последовательного приближения ![]() , а за следующее приближение
, а за следующее приближение ![]() берём точку пересечения этой касательной с осью Ox.
берём точку пересечения этой касательной с осью Ox.
Таким образом, наклон прямой подстраивается на каждом шаге наилучшим образом (ведь кривизну графика, связанную с второй производной, мы не учитываем, и поэтому неизвестно, в какую сторону от касательной отклонится график).
Заметим, что по-другому идею метода Ньютона мы можем описать так: на каждом шаге вместо исходного уравнения ![]() мы решаем приближённое линеаризованное в точке
мы решаем приближённое линеаризованное в точке ![]() уравнение:
уравнение:
![]()
в котором левая часть – это многочлен Тейлора первого порядка для функции f(x) в точке ![]() , то есть линейная функция
, то есть линейная функция
![]() .
.
Решением линеаризованного уравнения ![]() служит следующее приближение
служит следующее приближение ![]() , в то время как решением исходного точного уравнения
, в то время как решением исходного точного уравнения ![]() служит искомый корень
служит искомый корень ![]() .
.