Различные точки области определения описывают уравнения различных типов.
Будем рассматривать область G, во всех точках которой уравнение имеет один и тот же тип. Через каждую точку области проходят две характеристики. Для уравнений гиперболического типа характеристики действительны и различны, для уравнений эллиптического типа – комплексно сопряженные, для уравнений параболического типа – действительны и совпадают между собой.
Пусть ![]() и
и ![]() – характеристики уравнения гиперболического типа. Полагая
– характеристики уравнения гиперболического типа. Полагая
![]()
и поделив уравнение (4.5) на коэффициент при ![]() после преобразований, получим уравнение вида:
после преобразований, получим уравнение вида:
![]() . (4.9)
. (4.9)
Мы получили каноническую форму уравнений гиперболического типа. Уравнения этого типа можно привести и к другой форме. Для этого положим:
![]() ;
; ![]() .
.
Тогда уравнение (4.9) примет вид:
![]() .
.
Для уравнений параболического типа уравнения (4.8) совпадают друг с другом, и мы получим один общий интеграл уравнения (4.7):
![]() .
.
Положим
![]() ,
,
где ![]() – любая, линейно независимая с
– любая, линейно независимая с ![]() , функция.
, функция.
После дальнейших преобразований получим каноническую форму уравнения параболического типа:
![]() . (4.10)
. (4.10)
В случае уравнения эллиптического типа уравнения (4.8) дают интегралы:
![]() ,
,
где ![]() и
и ![]() – комплексно сопряженные функции.
– комплексно сопряженные функции.
Чтобы избавится от мнимой составляющей, введем новые переменные:
![]() ,
,
после чего получим каноническую форму уравнения эллиптического типа:
![]() . (4.11)
. (4.11)
Если коэффициенты линейного уравнения постоянные, то характеристическое уравнение имеет решение:
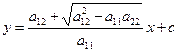 ;
;  .
.
В результате преобразования уравнение (4.3) приводится к одной из форм:
![]() (эллиптический тип);
(эллиптический тип);
![]() (гиперболический тип);
(гиперболический тип);
![]() (параболический тип).
(параболический тип).