Метод разделения переменных, или метод Фурье, или метод наложения стоячих волн, является одним из важнейших методов решения уравнений математической физики. Найдем решение задачи о свободных колебаниях конечной струны, закрепленной на концах, методом Фурье, то есть будем искать решение уравнения:

,                                           (4.31)

удовлетворяющее однородным или нулевым граничным условиям

 ,                                       (4.32)

и начальным условиям

 .                            (4.33)

Рассмотрим основную вспомогательную задачу.

Найти отличные от тождественного нуля решения уравнения (4.31), удовлетворяющие только граничным условиям (4.32), в виде произведения:

то есть в виде произведения функции только от x на функцию только от t. Такой подход дает возможность выбирать одну из функций  или  произвольно. Используя такой подход при решении уравнения (4.31), получим:

.

Поделив полученное выражение на , будем иметь:

.

Левая часть этого выражения зависит только от x, правая – только от переменного t. Так как последнее равенство справедливо для любых значений x и t (можно, например, зафиксировать x и менять t), то левая и правая части сохраняют постоянное значение, которое для удобства дальнейших выкладок обозначим так:

.

В результате получим два обыкновенных дифференциальных уравнения:

.                                             (4.34)

.                                             (4.35)

Учитывая граничные условия (4.32), получим:

;         .

Тогда

.                                                (4.36)

Нетрудно проверить, что если постоянная  отрицательна или равна нулю, то не существует отличной от тождественного нуля функции , удовлетворяющей краевым условиям (4.36). Поэтому постоянная  должна быть положительна. Для функции  в основной вспомогательной задаче дополнительных условий нет.

Задача решения уравнения (4.34) с условиями (4.36) называется задачей о собственных значениях или задачей Штурма-Лиувилля.

Ненулевое решение уравнения (4.34) запишется в виде:

.

Из граничных условий находим:

;        

Так как , то , поэтому . Отсюда

Следовательно,

.

Числа  называются собственными значениями краевой задачи (задачи Штурма-Лиувилля). Им соответствуют функции:

,

где  – произвольные постоянные, которые называются собственными функциями.

Ввиду произвольности выбора одной из функций  или  положим .

Тем же собственным значениям будут соответствовать решения уравнения (4.35):

,

где ,  – произвольные постоянные.

Итак, частными решениями основной вспомогательной задачи будут функции:

.

Сумма частных решений также является решением этой задачи:

.                           (4.37)

Если определить  и  по начальным условиям (4.33), то тем самым мы найдем решение поставленной задачи (4.31) – (4.33).

Подставив  в выражение (4.37), получим:

 ,                                        (4.38)

аналогично для производной :

 .                                      (4.39)

Чтобы найти  и , используем теорию рядов Фурье, из которой известно, что произвольная кусочно-непрерывная и кусочно-дифференцируемая функция , то есть функция, удовлетворяющая условиям Дирихле, заданная в промежутке , разлагается в ряд Фурье по синусам:

;       .

Если функции  и  удовлетворяют условиям Дирихле, то

;          ;

;         .

Сравнение этих рядов с формулами (4.38) и (4.39) показывает, что для выполнения начальных условий (4.33) надо положить:

.

Таким образом, окончательно, решение задачи о свободных колебаниях конечной струны с закрепленными концами имеет вид:

,

где

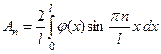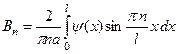 ;      .                (4.40)

Очевидно, ряд (4.40) должен сходиться, а функция  должна быть дифференцируемой. В противном случае выражение (4.40) не может быть решением рассматриваемого дифференциального уравнения.