Сформулируем задачу Коши для однородного уравнения (4.65):
. (4.66)
Если стержень очень длинный, то на процессы, протекающие в его средней части, главное влияние оказывает начальное распределение температуры; влияние температурных условий на концах стержня в течение довольно длительного времени почти не будет сказываться. В задачах такого типа стержень считают бесконечным. Краевые условия при этом отпадают, и на искомую функцию 
накладываются только начальные условия.
Задача Коши для однородного уравнения состоит в том, чтобы найти функцию , удовлетворяющую уравнению (4.66) и единственному начальному условию:
. (4.67)
Прежде чем решить уравнение (4.66) при начальном условии (4.67), мы несколько упростим задачу, введя вместо времени t новую переменную:
. (4.68)
Тогда 
, и уравнение (4.66) примет вид:
, (4.69)
не зависящий от физических свойств стержня. Так как при 
и 
, то в качестве начального условия мы будем иметь:
(4.70)
Чтобы решить эту задачу, применим метод Фурье. Этот метод состоит из двух частей. Будем искать частные решения уравнения (4.69) в виде произведение двух функций 
, каждая из которых зависит только от одной из независимых переменных. Подставляя это произведение вместо u в уравнение (4.69), получим:
,
или
. (4.71)
Обе части уравнения (4.71) должны быть постоянными, поскольку его левая часть не зависит от x, а правая не зависит от 
. Обозначим постоянную, которой должны быть равны левая и правая части равенства (4.71), через с. Тогда уравнение распадается на два уравнения:
; 
. (4.72)
Первое из них имеет общее решение:
.
Поскольку ни в одном сечении стержня (т.е. ни при каком фиксированном x) температура 
не может неограниченно возрастать по абсолютной величине при 
, то с должна быть отрицательна. Положим 
. Тогда
.
Второе из уравнений (4.72) принимает вид:
и имеет общее решение
.
Таким образом, мы получили частное решение уравнения (4.69):
или
,
где 
и 
.
Так как С, А, В – произвольные постоянные относительно x и t, то 
и 
могут зависеть от 
:
, 
.
Таким образом, окончательно семейство частных решений уравнения (4.69) будет иметь следующий вид:
. (4.73)
Ввиду отсутствия краевых условий (стержень бесконечен) может принимать произвольные значения от 
до 
. Поэтому вместо суммирования (которое применялось в методе Фурье при наложении стоячих волн, имеющих дискретные собственные частоты) мы должны здесь налагать решения 
непрерывно, то есть образовать решение уравнения (4.69) интегрированием по в пределах от до :
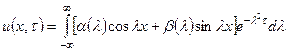. (4.74)
Функция (4.74) является решением уравнения (4.69), если несобственный интеграл (4.74) сходится и может быть продифференцирован по x и t под знаком интеграла.
Остается только подобрать неизвестные функции 
и 
так, чтобы решение уравнения (4.74) удовлетворяло начальному условию (4.70), т.е. чтобы
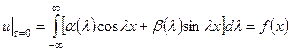. (4.75)
Последнее равенство означает, что функцию 
надо представить в виде интеграла (4.75). Эта задача решается интегралом Фурье, который является интегральным аналогом ряда Фурье.
Воспользуемся следующим утверждением. Если непрерывную на всей оси Ox функцию , можно разложить в ряд Фурье на любом конечном интервале и если интеграл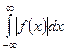 
сходится, т.е., как говорят, функция 
абсолютно интегрируема на всей оси Ох, то она может быть представлена в виде интеграла Фурье:
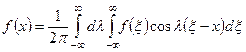. (4.76)
Или, так как
,
то формулу (4.76) можно переписать в виде:
.
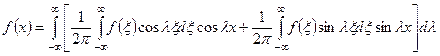Окончательно будем иметь:
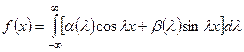, (4.77)
где
; 
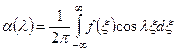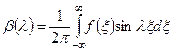. (4.78)
Таким образом, очевидно, что для уравнения (4.66) начальное условие (4.67) будет удовлетворено, если коэффициенты 
и 
определены по формулам (4.78). Поэтому, возвращаясь к старой переменной t, по формуле (4.74) получим:
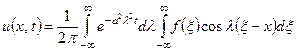. (4.79)