Перейдем к решению задачи Коши для неоднородного одномерного уравнения теплопроводности (4.65) при начальном условии (4.67). Представим функцию ![]() в виде интеграла Фурье, используя формулы (4.77) и (4.78):
в виде интеграла Фурье, используя формулы (4.77) и (4.78):
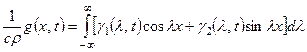 , (4.80)
, (4.80)
где
 ;
; 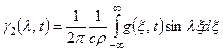 , (4.81)
, (4.81)
и будем искать решение в виде:
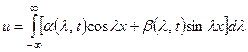 . (4.82)
. (4.82)
Подставляя выражение (4.82) в формулу (4.65), найдем:
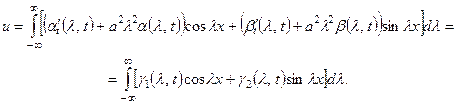
Очевидно, последнее равенство будет выполняться, если положить, для всех ![]() :
:
![]() ,
, ![]() . (4.83)
. (4.83)
Далее потребуем, чтобы функция (4.82) удовлетворяла начальному условию (4.67). Для этого нужно, чтобы
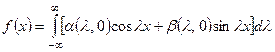 ,
,
то есть
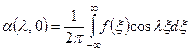 ,
, 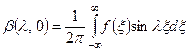 . (4.84)
. (4.84)
Из обыкновенных дифференциальных уравнений (4.83) при начальных условиях (4.84) найдем:
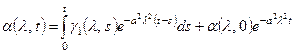 ;
;
 .
.
Подставляя эти выражения в формулу (4.82) и учитывая формулы (4.81), получим искомое решение:
![]()
![]()
![]()
![]() . (4.85)
. (4.85)
Формула (4.85) показывает, что решение в данном случае является суммой решения однородного уравнения (4.66), удовлетворяющего начальному условию (4.65) и решения неоднородного уравнения (4.65), удовлетворяющего нулевому начальному условию (этот факт имеет место для любых линейных дифференциальных уравнений).
Таким образом, температура в стержне складывается из температуры, которая была бы в момент t в точке x при наличие начальных температур, но при отсутствии источников тепла в стержне, и из температуры, которая была бы при наличие источников тепла, но при нулевой начальной температуре.