Пример 2.1
Небольшая фабрика изготавливает два вида красок: для внутренних работ – краска 1, и для внешних работ – краска 2. Продукция поступает в оптовую продажу. Для производства красок используется два вида сырья – A, B. Суточные запасы сырья составляют 6 и 8 центнеров соответственно. Расходы сырья на изготовление одного центнера красок 1, 2 и запасы приведены в таблице 2.1.
Таблица 2.1
|
Сырье |
Расход сырья (в центнерах) на центнер краски |
Запасы сырья (в центнерах) |
|
|
Краска 1 |
Краска 2 |
||
|
A B |
1 2 |
2 1 |
6 8 |
Изучение рынка сбыта показало, что суточный спрос на краску 2 никогда не превышает спроса на краску 1 более чем на 1 ц. Кроме того, установлено, что спрос на краску 1 никогда не превышает 2 ц. в сутки.
Оптовые цены одного центнера красок равны: 3 тыс. руб. для краски 1 и 2 тыс. руб. для краски 2.
Какое количество краски должна производить фабрика, чтобы доход от реализации продукции был максимальным?
Процесс построения модели можно начать с ответа на 3 вопроса:
1) Для определения каких величин должна быть построена модель? Другими словами, как идентифицировать переменные (искомые величины – эндогенные переменные) данной задачи?
2) Какие ограничения должны быть наложены на переменные, чтобы выполнялись условия, характерные для моделируемой системы (назначение параметров и экзогенных переменных)?
3) В чем состоит цель, для достижения которой из всех допустимых значений переменных нужно выбрать те, которые будут соответствовать оптимальному (наилучшему) решению задачи?
Эндогенные переменные:
Обозначим ![]() ,
, ![]() – суточные объемы выпуска красок 1 и 2 соответственно (в центнерах).
– суточные объемы выпуска красок 1 и 2 соответственно (в центнерах).
 |
Ограничения:
Из этого условия получаем:
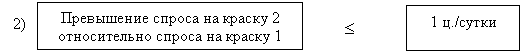 |
для сырья A ![]() ; для сырья B
; для сырья B ![]() .
.
Отсюда следует:
![]() .
.
Это условие равносильно неравенству:
![]() .
.
Неявное ограничение заключается в том, что объемы производства не могут быть отрицательными, т. е. ![]() ,
, ![]() .
.
Целевая функция
Так как стоимость одного центнера краски 1 равна 3 тыс. руб., то доход от ее реализации составит 3 тыс. руб. Аналогично, доход от реализации одного центнера краски 2 составит 2 тыс. руб.
При допущении о независимости рынка сбыта красок 1, 2 суммарный доход будет равен: ![]() .
.
Итак, получаем математическую модель.
Определить суточные объемы производства ![]() ,
, ![]() , при которых достигается максимум величины
, при которых достигается максимум величины ![]() (целевая функция), при ограничениях:
(целевая функция), при ограничениях:
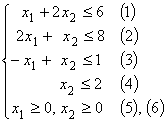 . (2.1)
. (2.1)