Пусть на плоскости задана прямоугольная система координат х1 и х2. Тогда каждому плану производства будет соответствовать на этой плоскости точка (х1, х2). Ясно, что не все точки на плоскости могут быть планами выпуска продукции, так как х1 и х2 связаны. Для определения допустимых планов выпуска краски, построим на этой плоскости множество точек, каждая из которых удовлетворяет системе ограничений.
Из аналитической геометрии известно, что любая линия на плоскости с уравнением g(х1, х2) = 0 разбивает плоскость на 2 части, в одной из которых выполняется неравенство g(х1, х2) < 0, а в другой – g(х1, х2) > 0. Сама линия является граничной для этих областей.
Построим граничные линии, соответствующие неравенствам (2.1), по точкам пересечения с осями координат (рис 2.1):
|
ограничение (1): х1 + 2х2 = 6, |
х1 |
0 |
6 |
|
х2 |
3 |
0 |
|
ограничение (2): 2х1 + х2 = 8, |
х1 |
0 |
4 |
|
х2 |
8 |
0 |
|
ограничение (3): –х1 + х2 = 1,
|
х1 |
0 |
–1 |
|
х2 |
1 |
0 |
 |
ограничение (4): х2 = 2 – прямая параллельная оси ![]() , ограничения (5) и (6) соответствуют координатным осям.
, ограничения (5) и (6) соответствуют координатным осям.
Стрелки указаны в сторону допустимых значений (рис. 2.1), таким образом, допустимое множество решений – многоугольник ![]() . Пространство решений содержит бесконечное множество решений, но можно найти оптимальное (наилучшее) решение, если выяснить, в каком направлении увеличивается целевая функция:
. Пространство решений содержит бесконечное множество решений, но можно найти оптимальное (наилучшее) решение, если выяснить, в каком направлении увеличивается целевая функция:
![]() .
.
 С этой целью на плоскость наносятся параллельные линии при нескольких последовательно возрастающих значениях целевой функции
С этой целью на плоскость наносятся параллельные линии при нескольких последовательно возрастающих значениях целевой функции ![]() , что позволяет определить наклон линий уровня целевой функции и направление, в котором происходит ее увеличение. Пусть, например, эти значения равны: 6, 9, 12 (рис. 2.2).
, что позволяет определить наклон линий уровня целевой функции и направление, в котором происходит ее увеличение. Пусть, например, эти значения равны: 6, 9, 12 (рис. 2.2).
При ![]() получаем прямую
получаем прямую ![]() ; при
; при ![]() :
: ![]() ; при
; при ![]() :
: ![]() . Эти прямые строим по точкам пересечения с осями координат. Все полученные прямые перпендикулярны одному и тому же вектору
. Эти прямые строим по точкам пересечения с осями координат. Все полученные прямые перпендикулярны одному и тому же вектору ![]() , координаты которого равны коэффициентам при неизвестных в целевой функции (ценам за единицу продукции). Для решения задачи необходимо найти точку области
, координаты которого равны коэффициентам при неизвестных в целевой функции (ценам за единицу продукции). Для решения задачи необходимо найти точку области ![]() , наиболее удаленную от начала координат в направлении вектора
, наиболее удаленную от начала координат в направлении вектора ![]() ..
..
Оптимальному решению соответствует угловая точка пространства допустимых решений – это точка ![]() .
.
Так как точка С является пересечением прямых (1) и (2), то оптимальные значения ![]() и
и ![]() будут решением системы уравнений С:
будут решением системы уравнений С: 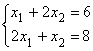 , решая которую, находим:
, решая которую, находим:
![]() ;
; ![]() .
.
Доход, получаемый при этом, будет равен:
![]() тыс. руб.
тыс. руб.
Везде в дальнейшем индекс * будет атрибутом оптимального решения.
Таким образом, ![]() – значение целевой функции при оптимальном решении (плане производства);
– значение целевой функции при оптимальном решении (плане производства); ![]() .
.