Анализируя примеры задач ЛП предыдущего раздела можно сделать вывод: в различных моделях решается задача на нахождение либо максимума, либо минимума целевой функции; левые и правые части ограничений могут быть связаны знаками: ![]() ,
, ![]() ,
, ![]() , кроме того, переменные
, кроме того, переменные ![]() в задаче ЛП могут не иметь ограничения в знаке. Поэтому для построения общего метода решения задачи ЛП ее необходимо представить в некоторой стандартной форме. При стандартной форме задачи ЛП:
в задаче ЛП могут не иметь ограничения в знаке. Поэтому для построения общего метода решения задачи ЛП ее необходимо представить в некоторой стандартной форме. При стандартной форме задачи ЛП:
 1) целевая функция подлежит максимизации;
1) целевая функция подлежит максимизации;
2) все ограничения записываются в виде равенств с неотрицательной правой частью;
3) все переменные заменяются неотрицательными.
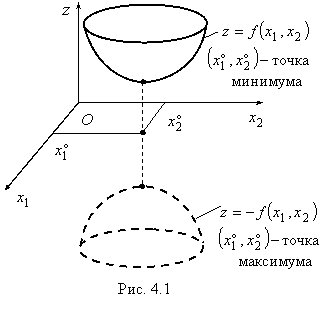
В первом случае, если в исходной постановке требуется найти минимум целевой функции, то ее можно заменить задачей на нахождение максимума функции ![]() , так как точки экстремума у этих функций совпадают. Например, если
, так как точки экстремума у этих функций совпадают. Например, если ![]() – точка минимума для функции двух переменных
– точка минимума для функции двух переменных ![]() , то она же является точкой максимума для функции
, то она же является точкой максимума для функции ![]() (рис. 4.1)
(рис. 4.1)
Во втором случае, если в системе ограничений присутствуют ограничения – неравенства, то в левую часть каждого такого ограничения добавляется или из неё вычитается неотрицательная дополнительная (балансовая) переменная ![]() (диапазон изменения индекса
(диапазон изменения индекса ![]() определяется по числу ограничений-неравенств).
определяется по числу ограничений-неравенств).
Если в системе ограничений присутствует неравенство вида:
![]() ,
,
то оно заменяется равенством
![]() , где
, где ![]() .
.
Аналогично, если в системе ограничений присутствует неравенство вида:
![]() ,
,
то оно заменяется равенством
![]() , где
, где ![]() .
.
В третьем случае, если какая-либо переменная ![]() не имеет ограничений в знаке, т.е. может быть как положительной, так и отрицательной, то вместо нее рассматриваются две других неотрицательных переменных
не имеет ограничений в знаке, т.е. может быть как положительной, так и отрицательной, то вместо нее рассматриваются две других неотрицательных переменных ![]() , которые связаны с переменной
, которые связаны с переменной ![]() равенствами:
равенствами:
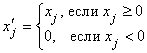 ;
; 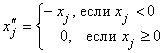 ;
;
тогда ![]() .
.
Например, задача оптимизации производства в стандартной записи будет иметь вид:
![]()
при условиях:
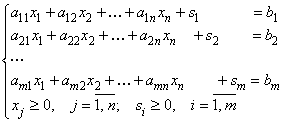 .
.
Обозначим общее количество переменных в стандартной форме через ![]() , а число ограничений-равенств обозначим через
, а число ограничений-равенств обозначим через ![]() (например, в задаче оптимизации производства
(например, в задаче оптимизации производства ![]() ). Эти обозначения будут использоваться и в дальнейшем.
). Эти обозначения будут использоваться и в дальнейшем.
Анализируя пример 2.1, можно сделать вывод, что оптимальному решению соответствует одна из угловых точек множества допустимых решений. В силу линейности целевой функции и ограничений в общем случае это тоже будет так, т.е. оптимальным решением является одна из угловых точек многогранника решений. Именно этот результат положен в основу симплекс-метода, основного метода решения задач ЛП. В его вычислительной схеме реализуется упорядоченный процесс, при котором, начиная с некоторого исходного допустимого решения (допустимой угловой точки), осуществляются последовательные переходы от одной угловой точки к другой до тех пор, пока не будет найдено оптимальное решение.
Выбор каждой очередной угловой точки при использовании симплекс-метода определяется правилами:
1. Каждая последующая угловая точка должна быть смежной с предыдущей.
2. Обратный переход к предшествующей допустимой точке производиться не может.
В примере 2.1 начальное допустимое решение – начало координат (см. рис 2.1). От исходной точки осуществляется переход к некоторой смежной угловой точке, т.е. либо к точке B, либо к точке F. Выбор зависит от коэффициентов целевой функции. Так как коэффициент при переменной ![]() больше коэффициента при переменной
больше коэффициента при переменной ![]() , а целевая функция максимизируется, то требуемое направление – это направление к точке B. После чего процесс повторяется, и рассматриваются точки, смежные с точкой B, и выясняется, есть ли другая угловая точка, соответствующая лучшему значению целевой функции.
, а целевая функция максимизируется, то требуемое направление – это направление к точке B. После чего процесс повторяется, и рассматриваются точки, смежные с точкой B, и выясняется, есть ли другая угловая точка, соответствующая лучшему значению целевой функции.