Теперь, для реализации симплекс-метода, угловые точки множества допустимых решений необходимо представить в алгебраической форме (в виде системы равенств).
Рассмотрим, прежде всего, этот вопрос на примере 2.1. Запишем стандартную форму задачи. Она будет иметь вид:
![]()
при ограничениях
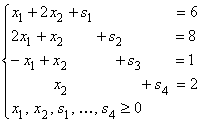 . (4.1)
. (4.1)
Здесь число переменных равно: ![]() число ограничений-равенств:
число ограничений-равенств: ![]() .
.
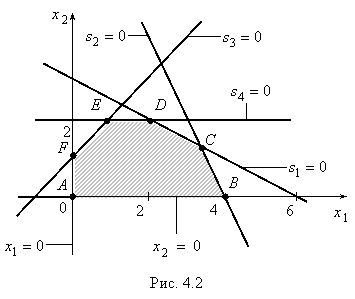
Теперь, как нетрудно убедиться, каждая из граничных линий множества допустимых решений определяется либо равенством ![]() , либо равенством
, либо равенством ![]() рис. (4.2). Таким образом, каждая угловая точка множества допустимых решений, как точка пересечения двух прямых, задается системой равенств нулю двух переменных. Описание угловых точек приведено в таблице 4.1.
рис. (4.2). Таким образом, каждая угловая точка множества допустимых решений, как точка пересечения двух прямых, задается системой равенств нулю двух переменных. Описание угловых точек приведено в таблице 4.1.
|
Таблица 4.1 |
||
|
Угловая точка |
Переменные |
|
|
нулевые |
ненулевые |
|
|
| ||