Предположим, что величина запаса ресурса первого вида (А) увеличена на .

Введение добавки в правую часть первого ограничения, означает увеличение балансовой переменной  на . Следовательно, с добавкой  в последнем столбце будут выполняться те же самые преобразования, что и с элементами столбца "". Все преобразования симплекс-таблиц, т.е. решение задачи симплекс-методом, приведут к изменению последнего столбца, в котором появится добавки  с коэффициентами из столбца "". Поэтому для получения нового решения с  в правой части первого ограничения, необходимо к элементам столбца "Решение" добавить величину  с коэффициентами из столбца "". Введение  сказывается только на правой части ограничений, и изменение запаса первого ресурса может повлиять только на допустимость решения. Поэтому величина  не может принимать значений, при которых, какая-либо переменная становится отрицательной.

Записывая это условие, получим систему неравенств:

  ,

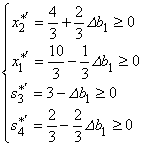здесь  – новые оптимальные значения переменных, 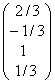 – столбец "" (табл. 4.5). Решая систему, получим, что . При этом:

.

Аналогично, увеличивая ресурс второго вида на величину , получаем систему неравенств:

,

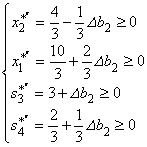из которой находим . При этом:

.