Некоторый однородный продукт; сосредоточенный у m поставщиков , в количестве единиц () необходимо доставить п потребителям , в количестве единиц (). Известна стоимость перевозки единицы груза от i-го поставщика к j-му потребителю.

Необходимо составить план перевозок, позволяющий вывезти все грузы, полностью удовлетворить потребности и имеющий минимальную стоимость.

Обозначим через количество единиц груза, запланированных к перевозке от i-го поставщика к j-му потребителю; тогда условие задачи можно записать в виде таблицы (табл. 8.1), которую в дальнейшем будем называть матрицей планирования.

Составим математическую модель задачи. Так как от i-го поставщика к j-му потребителю запланировано к перевозке единиц груза, то стоимость перевозки составит: . Стоимость всего плана выразится двойной суммой:

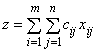
Систему ограничений получаем из следующих условий задачи:

а) все грузы должны быть вывезены, т. е.

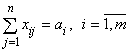                                                 (8.1)

(левые части этих уравнений получаются суммированием по строкам табл. 8.1);

б) все потребности должны быть удовлетворены, т.е.

                                            (8.2)

(левые части этих уравнений получаются суммированием по столбцам табл. 8.1).

Таким образом, математическая модель транспортной задачи имеет следующий вид.

Найти наименьшее значение линейной функции

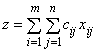                                                  (8.3)

при ограничениях:

.

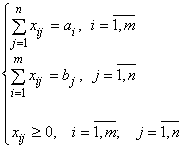В рассмотренной модели предполагается, что суммарные запасы равны суммарным потребностям, т.е.

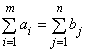.                                                     (8.4)

Такая модель называется закрытой или сбалансированной. Если равенство (8.4) не выполняется, то модель называется открытой или несбалансированной.

Для открытой модели может быть два случая:

а) суммарные запасы превышают суммарные потребности

;

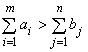б) суммарные потребности превышают суммарные запасы

.

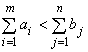Линейная функция одинакова в обоих случаях, изменяется только вид системы ограничений:

случай а) 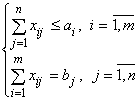   ;           случай б)     .

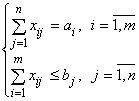Открытая модель решается приведением к закрытой модели следующим образом.

В случае а, когда суммарные запасы превышают суммарные потребности, вводится фиктивный потребитель , потребности которого:

.

В случае б, когда суммарные потребности превышают суммарные запасы, вводится фиктивный поставщик  запасы которого:

.

Стоимость перевозки единицы груза как до фиктивного потребителя, так и стоимость перевозки единицы груза от фиктивного поставщика полагают равными нулю, так как груз в обоих случаях не перевозится.

После преобразования задача принимает вид закрытой модели и решается обычным способом. При равных стоимостях перевозки единицы груза от поставщиков к фиктивному потребителю затраты на перевозку груза реальным потребителям минимальны, а фиктивному потребителю будет направлен груз от наименее выгодных поставщиков. То же самое получаем и в отношении фиктивного поставщика.

Прежде чем решать какую-нибудь транспортную задачу, необходимо сначала проверить, к какой модели она принадлежит, и только после этого составлять таблицу для ее решения.

Теорема 8.1

Любая транспортная задача, у которой суммарный объем запасов совпадает с суммарным объемом потребностей, имеет решение.

Доказательство. Для доказательства теоремы необходимо показать, что при заданных условиях существует хотя бы один допустимый план перевозок и линейная функция на множестве планов ограничена.

Пусть , где . Тогда величины  являются планом, так как они удовлетворяют системе ограничений (8.1), (8.2). Действительно, подставляя значения  в формулы (8.1) и (8.2), получим:

;   .

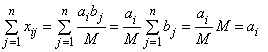Теперь, выберем из значений  наибольшее  и заменим в линейной функции (8.3) все коэффициенты на , тогда, учитывая (8.1), получим:

.

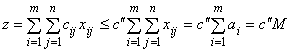Выберем из значений  наименьшее  и заменим в линейной функции все коэффициенты на , тогда, учитывая (8.1), получим:

.

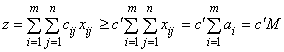Объединяя два последних неравенства в одно двойное, окончательно получим:

,

т.е. линейная функция ограничена на множестве допустимых планов транспортной задачи, и теорема доказана.