Семантика исчисления L определяется с помощью произвольной функции е:S![]() {0,1}=I, удовлетворяющей для всех А,В
{0,1}=I, удовлетворяющей для всех А,В![]() S соотношениям
S соотношениям ![]() и е(А
и е(А![]() В)=е(А)
В)=е(А) ![]() е(В).
е(В).
Функция е называется интерпретацией исчисления L.
Лемма 1 (об интерпретации исчисления L). Для каждой функции f: Р![]() I, заданной на множестве букв исчисления L, существует единственная интерпретация еf: S
I, заданной на множестве букв исчисления L, существует единственная интерпретация еf: S![]() I исчисления L, ограничение которой на Р равно f, в том смысле, что еf(p) = f(p), для всех p
I исчисления L, ограничение которой на Р равно f, в том смысле, что еf(p) = f(p), для всех p ![]() P.
P.
Доказательство. Пусть S0 = P, Sn+1 = Sn![]() {
{![]() A: A
A: A![]() Sn}
Sn}![]() {(A
{(A![]() B):A,B
B):A,B![]() Sn}. Утверждение леммы доказывается по индукции. Положим ef(A)=f(A) для A
Sn}. Утверждение леммы доказывается по индукции. Положим ef(A)=f(A) для A![]() S0. Предполагая, что ef уже определена на Sn, продолжим её на Sn+1 следующим образом: Если А=
S0. Предполагая, что ef уже определена на Sn, продолжим её на Sn+1 следующим образом: Если А=![]() В, для некоторого В
В, для некоторого В![]() Sn, то положим ef(A) =
Sn, то положим ef(A) =![]() ; аналогично, в случае A=(B
; аналогично, в случае A=(B![]() C) при некоторых В, С
C) при некоторых В, С![]() Sn, положим ef(B
Sn, положим ef(B![]() C) = ef(B)
C) = ef(B) ![]() ef(C). В результате получаем функцию
ef(C). В результате получаем функцию 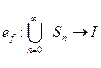 , ограничение которой на Р равно f.
, ограничение которой на Р равно f.
Формула А исчисления L называется тавтологией, если е(А)=1, для любой интерпретации е:S![]() I исчисления L.
I исчисления L.
Теорема (о полноте). Формула А исчисления высказываний L является тавтологией тогда и только тогда, когда она является теоремой исчисления L.
Доказательство. Если формула А является теоремой исчисления L, то, поскольку аксиомы являются тавтологиями и применение MP к тавтологиям Р и Р![]() Q даёт тавтологию, мы можем заключить, что А – тавтология. Это доказывает, что каждая теорема является тавтологией. Для доказательства обратного утверждения нам понадобится следующая лемма.
Q даёт тавтологию, мы можем заключить, что А – тавтология. Это доказывает, что каждая теорема является тавтологией. Для доказательства обратного утверждения нам понадобится следующая лемма.
Лемма 2. Пусть формула А содержит переменные а1, а2, …, аn, и пусть задана некоторая функция f: { а1,а2,…,аn }![]() I={0,1}. Тогда
I={0,1}. Тогда ![]()
![]() L А’, где
L А’, где ![]() и А’ обозначают следующие формулы:
и А’ обозначают следующие формулы:
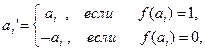
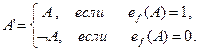
Здесь ef обозначает интерпретацию исчисления L для случая, когда Р={ а1,а2,…,аn}, по лемме об интерпретации ef определяется функцией f единственным образом.
Доказательство леммы проведем по индукции, по количеству логических связок ![]() и
и ![]() в формуле А. В случае, когда А = а – переменная, имеем: а
в формуле А. В случае, когда А = а – переменная, имеем: а ![]() L а и
L а и ![]() а
а ![]() L
L![]() а.
а.
Пусть А = ![]() В. Если ef(B) = 1, то ef(A) = 0 и А’ =
В. Если ef(B) = 1, то ef(A) = 0 и А’ = ![]() А =
А = ![]()
![]() В. По предположению индукции
В. По предположению индукции ![]()
![]() L В. Пользуясь теоремой
L В. Пользуясь теоремой ![]() L В
L В![]()
![]()
![]() В, получаем:
В, получаем: ![]()
![]() L
L ![]()
![]() В = А’. Если же ef(B) = 0, то ef(A) = 1 и А’ = А=
В = А’. Если же ef(B) = 0, то ef(A) = 1 и А’ = А= ![]() В. По предположению индукции:
В. По предположению индукции: ![]()
![]() L
L ![]() В и
В и ![]() В =А’.
В =А’.
Рассмотрим случай А = (В![]() С). По предположению индукции:
С). По предположению индукции:
![]()
![]() L В’ и
L В’ и ![]()
![]() L С’.
L С’.
Если ef(B) = 0, то независимо от значения ef(C) имеем: ef(A)=1 и В’ = ![]() В, А’ = А. Но
В, А’ = А. Но ![]()
![]() L
L ![]() В. С помощью теоремы
В. С помощью теоремы ![]() L
L ![]() В
В![]() (В
(В![]() С), получаем:
С), получаем: ![]()
![]() L В
L В![]() С.
С.
Если ef(B) = 1 , то возможны 2 случая: – ef(C) = 1 или ef(C) = 0. В случае ef(C) = 1 имеем: ef(A) = 1 и С’ = С, А’ = А = (В![]() С). Имеем:
С). Имеем: ![]()
![]() L С и
L С и ![]() L С
L С![]() (В
(В![]() С) (по аксиоме А1), следовательно,
С) (по аксиоме А1), следовательно, ![]()
![]() L В
L В![]() С. В случае ef(В) = 1 и ef(С) = 0 имеют место: А’ =
С. В случае ef(В) = 1 и ef(С) = 0 имеют место: А’ =![]() A=
A=![]() (B
(B![]() C), B’ = B, C’ =
C), B’ = B, C’ =![]() C. Имеем:
C. Имеем:
![]()
![]() L В,
L В, ![]()
![]() L
L ![]() С.
С.
Пользуясь теоремой ![]() L В
L В![]() (
(![]() С
С![]()
![]() (В
(В![]() С)), получаем:
С)), получаем:
![]()
![]() L
L ![]() (В
(В![]() С) =А’. Лемма доказана.
С) =А’. Лемма доказана.
Вернёмся к доказательству теоремы о полноте. Пусть А – тавтология. Тогда по доказанной лемме: ![]()
![]() L А, ибо ef(A) = 1 для любой интерпретации букв
L А, ибо ef(A) = 1 для любой интерпретации букв ![]() . Значит, существуют выводы:
. Значит, существуют выводы: ![]()
![]() L А, и
L А, и ![]()
![]() L А . По теореме о дедукции:
L А . По теореме о дедукции: ![]()
![]() L аn
L аn![]() А и
А и ![]()
![]() L
L ![]() an
an![]() А. Пользуясь теоремой
А. Пользуясь теоремой ![]() L (аn
L (аn![]() А)
А) ![]() ((
((![]() аn
аn![]() А)
А) ![]() А) и применяя MP, получаем:
А) и применяя MP, получаем: ![]()
![]() L А. Повторяя этот процесс ещё n – 1 раз, приходим к теореме:
L А. Повторяя этот процесс ещё n – 1 раз, приходим к теореме: ![]() L А, что и требовалось доказать.
L А, что и требовалось доказать.
Упражнение
Доказать выводимость формул:
![]() L В
L В![]()
![]()
![]() В,
В,
![]() L
L ![]() В
В![]() (В
(В![]() С),
С),
![]() L В
L В![]() (
(![]() С
С![]()
![]() (В
(В![]() С))
С))
Следствие (теорема о непротиворечивости). Исчисление высказываний L непротиворечиво в том смысле, что не существует формулы А исчисления L, для которых А и ![]() А были бы теоремами.
А были бы теоремами.
Доказательство. По теореме о полноте, каждая теорема исчисления является тавтологией. Но отрицание тавтологии не является тавтологией, значит, ни для какой формулы А невозможно, чтобы А и ![]() А были теоремами
А были теоремами
.