Пусть U – произвольное множество. Будем рассматривать его подмножества и U будем называть универсумом. Каждое подмножество описывается с помощью свойств его элементов. Например, в универсуме натуральных чисел w подмножество {0, 1, 2, 3, 4, 5} задаётся как

A = {n Î w: n £ 5}.

Его можно определить с помощью характеристической функции , принимающей значения:

Проблема возникает при попытке определения подмножества чисел, указывающих значение возраста, при которых человек считается старым.

Пусть [0, 1] = {r Î R : 0 £ r £ 1} – единичный отрезок действительных чисел.

Определение. Нечетким множеством m на универсуме U называется произвольная функция m : U ® [0, 1]. Множество всех нечетких множеств на U обозначается через F(U).

Заметим, что часто понятия нечёткого множества и определяющей его функции различают. В этом случае, говоря о нечётком множестве A, имеют в виду функцию . Обозначают эту функцию через  и называют её функцией принадлежности.

Значение m(x) называется степенью принадлежности x нечеткому множеству m. Например, нечеткое множество «старый» определяется как функция , для которой m(70) = 1, а m(0) = 0, ибо ясно, что человек семидесяти лет является старым, а не достигнувший одного года младенец – нет. Можно считать, что m(20) = 0. Возрасту 45 лет можно приписать значение m(45) = 0.5, и далее продолжить функцию m линейно на интервале [20, 70].

Представление нечетких множеств

Существуют различные методы описания функции m : U ® [0, 1]. Если U – конечное множество, то функция будет конечным множеством пар:

m = {(x₁, m(x₁)), …, (x_n, m(x_n))}.

и может быть записана как

m = m(x₁)/x₁ + … + m(x_n)/x_n

или в виде таблицы:

В случае универсума R действительных чисел m(x) задаётся аналитически и изображается в виде графика. Например,  будет гауссианой, с m(a) = 1. Лингвистическое выражение «большое число» обозначает понятие, зависящее от параметров, и может быть интерпретировано с помощью функции:

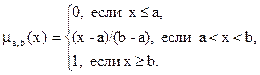
Определение. Пусть  и . Множество

называется a-срезом нечеткого множества m.

Теорема 1. Пусть , , . Тогда

1)

2) если a < b, то ,

3) .

Теорема 2 (о представлении). Пусть . Тогда

.

Нечеткие множества  называются равными, если  для всех ; m₁ называется нечетким подмножеством m₂, если  для всех , в этом случае применяется запись: .

Операции над нечеткими множествами

Пусть . Операции определяются следующим образом:

 (дополнение);

 (пересечение);

 (объединение);

 (ограниченное произведение);

 (ограниченная сумма);

 (алгебраическое произведение);

 (алгебраическая сумма);

 (разность);

 (концентрирование).

Поскольку каждое нечеткое множество m можно представить как семейство a-срезов, то операции можно выразить через обычные операции над множествами. В частности:

          (дополнение);

 (пересечение);

 (объединение);

Принцип обобщения

Произвольная функция  между множествами может быть расширена до функции  следующим образом:

.

Этот метод расширения называется принципом обобщения. Предполагается, что супремум пустого множества равен 0. С помощью принципа обобщения можно расширить операцию сложения , полагая для любых :

Нечеткое множество  называется выпуклым, если все его a-срезы выпуклы. Легко видеть, что сумма  нечётких выпуклых множеств m₁ и m₂ из R будет выпуклой.