Определение: Переменная величина z называется однозначной функцией двух переменных  х и у, если каждой точке (х, у), принадлежащей некоторому множеству D, соответствует одно определенное значение величины z.

Определение. Переменные х и у называются независимыми переменными или аргументами.

Определение Множество D называется областью определения функции.

Обозначения функции: z = f (х, у); z = j (х, у) и т.п.

Область определения функции в простейших случаях  представляет собой некоторое множество D точек плоскости Оху.

Геометрическим изображением функции z = f(х, у) (графиком) является некоторая поверхность.

Аналогично определяется функция любого числа переменных.

Пусть D – произвольное множество точек n-мерного арифметического пространства.

Если каждой точке Р(x₁, x₂, …, x_n), принадлежащей области D поставлено в соответствие единственное значение переменной z, то z называют функцией n переменных:

z = f(x₁, x₂, …, x_n)   или   z = f(P).

Линией уровня функции двух переменных z = f(x, y) называется линия плоскости Оху, в точках которой функция сохраняет постоянное значение  f(x, y) = С.

Поверхностью уровня функции трех переменных u = f(x, y, z) называется поверхность f(x, y, z) = С, в точках которой функция сохраняет постоянное значение.

Пример 1.1. Найти область определения функции z = arcsin(x/y²).

Решение. Функция  z = arcsin(x/y²) определена, если   и  ,  или   –у²  х  у². Областью определения функции является часть плоскости, заключенная между двумя параболами у² = х и у² = –х, за исключением точки О(0,0) (рис 1.1).

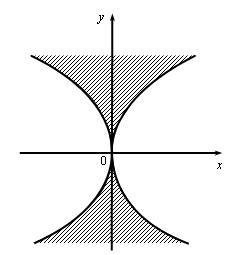
Рис. 1.1. Область определения функции z = arcsin(x/y²)

Пример 1.2. Найти область определения функции

.

Решение. Выражение

 имеет смысл,

когда R² – х² – у² – z²  0; а выражение

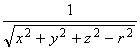
 существует, если х² + у² + z² – r² > 0.

Неравенство х² + у² + z²  R² определяет шар с центром в начале координат и радиусом .

Из неравенства  х² + у² + z² – r² > 0  имеем

х² + у² + z² > r².

Таким образом, областью определения функции  f(x, y, z)  является часть пространства, заключенная между сферами х² + у² + z² = r²  и  x² + у² + z² = R², причем поверхность внешней сферы входит в область определения, а поверхность внутренней сферы не входит.

Пример 1.3. Найти линии уровня функции  z = х²+ у².

Решение. Уравнение семейства линий уровня имеет вид

х² + у² = С   (С > 0).

Придавая С различные вещественные значения, получим концентрические окружности с центрами в начале координат.