Для упрощения записи и изложения материала ограничимся случаем функций двух переменных. Все дальнейшее справедливо также для функций любого числа переменных.
Определение. Частной производной функции z = f(х, у) по независимой переменной х называется производная
![]()
вычисленная при постоянном у.
Аналогично определяется частная производная по переменной у.
![]()
Для частных производных справедливы обычные правила и формулы дифференцирования.
Определение. Произведение частной производной ![]()
![]() на приращение аргумента
на приращение аргумента ![]() х (
х (![]() y) называется частным дифференциалом по переменной х (у) функции двух переменных z = f(x, y) (обозначения:
y) называется частным дифференциалом по переменной х (у) функции двух переменных z = f(x, y) (обозначения: ![]() ):
):
![]()
Если под дифференциалом независимой переменной dx (dy) понимать приращение ![]() х (
х (![]() у), то
у), то
![]()
Для функции z = f(x, y) выясним геометрический смысл ее частотных производных ![]() и
и ![]() .
.
Рассмотрим точку ![]() , точку P0(х0, y0, z0) на поверхности z = f(x, у) и кривую L, которая получится при сечении поверхности плоскостью у = у0. Эту кривую можно рассматривать как график функции одной переменной z = f(x, y) в плоскости у = у0. Если провести в точке Р0(х0, у0, z0) касательную к кривой L, то, согласно геометрическому смыслу производной функции одной переменной
, точку P0(х0, y0, z0) на поверхности z = f(x, у) и кривую L, которая получится при сечении поверхности плоскостью у = у0. Эту кривую можно рассматривать как график функции одной переменной z = f(x, y) в плоскости у = у0. Если провести в точке Р0(х0, у0, z0) касательную к кривой L, то, согласно геометрическому смыслу производной функции одной переменной ![]() , где a – угол, образованный касательной с положительным направлением оси Ох. Или:
, где a – угол, образованный касательной с положительным направлением оси Ох. Или: 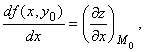 аналогично зафиксируем другую переменную, т.е. проведем сечение поверхности z = f(x, y) плоскостью х = х0. Тогда функцию
аналогично зафиксируем другую переменную, т.е. проведем сечение поверхности z = f(x, y) плоскостью х = х0. Тогда функцию
z = f(x0, y) можно рассмотреть как функцию одной переменной у:
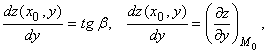
где b – угол, образованный касательной в точке М0(х0, у0) с положительным направлением оси Oy (рис. 1.2).
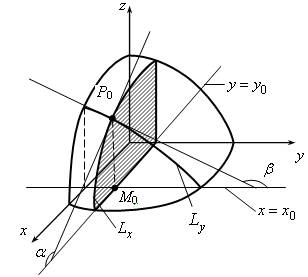
Рис. 1.2. Иллюстрация геометрического смысла частных производных
Пример 1.6. Дана функция z = х2 – 3ху – 4у 2 – х + 2у + 1. Найти ![]() и
и ![]() .
.
Решение. Рассматривая у как постоянную величину, получим
![]()
Считая х постоянной, находим
![]() .
.
Пример 1.7. Показать, что функция z = yln(x2 – у2) удовлетворяет уравнению:
![]()
Решение. Находим производные
![]()
Подставив частные производные в левую часть уравнения:

![]()
получаем тождество, т.е. функция z удовлетворяет данному уравнению.
Пример 1.8. Показать, что функция z удовлетворяет уравнению
![]()
Решение. ![]()
![]() .
.
Подставляем в уравнение:
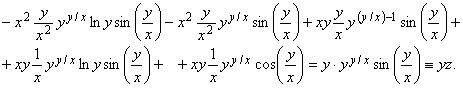
Получили тождество, т.е. функция z удовлетворяет уравнению.