Экстремум функции – это свойство местного, локального характера (см. определение). Не следует смешивать максимум (минимум) с наибольшим (наименьшим) значением функции в замкнутой области D.
Определение. Допустим, функция z = f(x, y) определена и непрерывна в некоторой области D, имеет в этой области конечные частные производные. Тогда в этой области найдутся точки, в которых функция достигает наибольшего и наименьшего значения остальных значений. Эти точки могут лежать внутри области или на ее границе.
Для того чтобы найти наибольшее и наименьшее значения функции в замкнутой области, нужно:
1) Найти стационарные точки, расположенные внутри области, и вычислить значения функции в этих точках.
Замечание. Присоединить к стационарным точкам точки, в которых производные бесконечны или не существуют (если такие имеются).
2) Найти стационарные точки на границе области и вычислить значения функции в этих точках.
3) Найти значения функции в угловых точках – точках пересечения граничных линий.
4) Из всех найденных значений выбрать наибольшее и наименьшее.
Пример 1.22. Найти наибольшее и наименьшее значение функции
z = 2x2 – xy + + y2 + 7x в замкнутой области D: –3 ![]() x
x ![]() 3, –3
3, –3 ![]() y
y ![]() 3 (рис. 1.3).
3 (рис. 1.3).
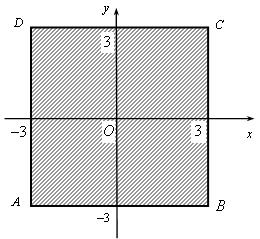
Рис. 1.3. Область исследования D
Решение. 1) Находим стационарные точки
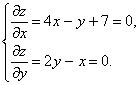
Отсюда у = –1, х = –2, стационарная точка М0(–2, –1) ![]() D, z(М0) = –7.
D, z(М0) = –7.
2) Исследуем функцию на границе области, которая состоит из отрезков AB, DC, CB, AD.
а) На прямой AB: у = 3, а функция имеет вид
z = 2x2 + 3x + 9 + 7x =
= 2x2 + 10x + 9, x ![]() [–3, 3].
[–3, 3].
Эта функция одной независимой переменной. Определим стационарные точки данной функции:
![]() следовательно, х = –2,5.
следовательно, х = –2,5.
Определяем z при х = –2,5, а также на концах отрезка [-3, 3]:
z (–2,5; –3) = –3,5; z(–3, –3) = –3; z(3, –3) = 57,
значит ![]() = 3,5, а
= 3,5, а ![]() = 57.
= 57.
б) Рассмотрим отрезок ВС: х = 3.
z = у2 – 3у + 39; у ![]() [–3, 3],
[–3, 3],
![]() = 2у – 3; 2у – 3 = 0
= 2у – 3; 2у – 3 = 0 ![]() у = 3/2.
у = 3/2.
Находим z(3, 3/2) =![]() , z(–3, 3) = 15, z(3, 3) = 39.
, z(–3, 3) = 15, z(3, 3) = 39.
![]() = 15,
= 15, ![]() = 39.
= 39.
в) На отрезке CD: у = 3, z = 2x2 + 4x + 9; у ![]() [–3, 3],
[–3, 3],
![]() = –4x + 4 = 0 Þ x = –1; z(–1, 3) = 7, z(–3, 3) = 15, z(3, 3) = 39;
= –4x + 4 = 0 Þ x = –1; z(–1, 3) = 7, z(–3, 3) = 15, z(3, 3) = 39;
![]() = 7, а
= 7, а ![]() = 39.
= 39.
г) Аналогично на отрезке DA: х = –3, у Î [–3, 3], z = у2 + 3у – 3,
![]() = 2у + 3 = 0 Þ у =
= 2у + 3 = 0 Þ у = ![]() ;
;
z(–3, –3/2) = –5,25, z(–3, –3) = –3, z(–3, 3) = 15;
![]() = –5,25, а
= –5,25, а ![]() = 15.
= 15.
3) Теперь сравним все найденные значения со значением в стационарной точке. Получаем zнаим = –7 в стационарной точке (–2, –1), zнаиб = 57 в точке М(3, –3), которая принадлежит границе области D.