Рассмотрим функцию f(M) = f(x, y, z), её частные производные по х, у, z выражают "скорость изменения" функции по направлениям координатных осей. Например ![]() – есть "скорость изменения" функции по х (точка предполагается перемещающейся лишь по прямой, параллельной оси Ох). В некоторых задачах (физики, например) возникает вопрос об изменении функции по другим направлениям. Примером может служить скалярное поле температур в пространстве, занятом неравномерно нагретым телом.
– есть "скорость изменения" функции по х (точка предполагается перемещающейся лишь по прямой, параллельной оси Ох). В некоторых задачах (физики, например) возникает вопрос об изменении функции по другим направлениям. Примером может служить скалярное поле температур в пространстве, занятом неравномерно нагретым телом.
Замечание. Скалярное поле – это часть пространства, в каждой точке М(х, у, z) которого задана некоторая скалярная функция F(M) = F(x, y, z), т.е. каждой точке поставлено в соответствие число. Так, если тело нагрето неравномерно, то и температура в разных точка разная, следовательно Т = Т(М) – скалярное поле температур.
Рассмотрим пространственное скалярное поле f(М) и любую точку М0(х0, у0, z0) этого поля и произвольную ось l, проходящую через эту точку (рис. 1.4).
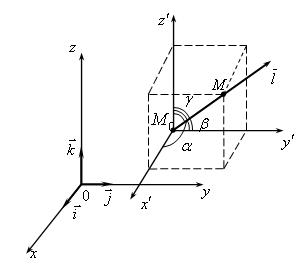
Рис. 1.4. Иллюстрация к определению производной по направлению
Определение. Пусть М – какая- либо другая точка оси. Составим разность
f(M) – f(M0) и разделим ее на расстояние r = |М0М|. Пусть точка М приближается к точке М0. Предел
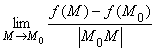
называется производной функции f(M) вдоль оси l, или по направлению l. Обозначается
![]()
Эта производная характеризует "скорость изменения" функции в точке М0 по направлению l. Обозначив через ![]() единичный вектор в направлении l, имеем
единичный вектор в направлении l, имеем
![]()
где ![]() – единичные векторы осей Ох, Оу и Оz соответственно; cosa, cosb, cosg – направляющие косинусы вектора
– единичные векторы осей Ох, Оу и Оz соответственно; cosa, cosb, cosg – направляющие косинусы вектора ![]() . Тогда
. Тогда
![]()
![]() Пример 1.23. Найти производную функции u = ху2z3 в точке М(3, 2, 1) в направлении вектора
Пример 1.23. Найти производную функции u = ху2z3 в точке М(3, 2, 1) в направлении вектора ![]() , где N(5, 4, 2).
, где N(5, 4, 2).
Решение. Находим вектор ![]() .
.
![]() =
= ![]() = (5 – 3)
= (5 – 3)![]() + (4 – 2)
+ (4 – 2)![]() + (2 –1)
+ (2 –1)![]() = 2
= 2![]() + 2
+ 2![]() +
+ ![]() .
.
Направляющие косинусы: ![]() аналогично cosb = 2/3; cosg = 1/3 .
аналогично cosb = 2/3; cosg = 1/3 .
Частные производные: ![]() .
.
Значения частных производных в точке ![]() :
:
![]()
Отсюда: ![]()