К числу весьма эффективных методов интегрирования относится метод интегрирования по частям.

Теорема 2.3. Пусть функции u(х) и v(x) непрерывны на некотором промежутке и дифференцируемы во всех его внутренних точках  и пусть функция  имеет первообразную на этом промежутке. Тогда на промежутке  функция также имеет первообразную и справедлива формула

   или                 (2.1)

Доказательство: Из равенства

следует, что

.

Первообразной  функции  на промежуткеявляется функция .Функция  имеет первообразную на по условию теоремы. Следовательно, и функция имеет  первообразную на промежутке . Интегрируем по-

следнее равенство. ■

Формула (2.1)  называется формулой интегрирования по частям. Ее применение целесообразно в тех случаях, когда подынтегральное выражение  удается представить в виде произведения двух сомножителей u и dv таким образом, чтобы интегрирование выражений dv и vdu являлось задачей более простой, чем интегрирование исходного выражения.

Иногда для вычисления интеграла формула интегрирования по частям применяется несколько раз.

Укажем некоторые часто встречающиеся интегралы, которые вычисляются методом интегрирования по частям.

1) Интегралы вида

где  – многочлен   n-ой степени,   k = const,  берутся  по  частям,  если    положить

u =  (после каждого интегрирования по частям степень многочлена понижается на единицу).

2) В интегралах вида

 за u при интегрировании по частям принимают функцию, являющуюся множителем при .

3) Интегралы вида

где a, b = const, находятся двукратным интегрированием по частям.

Пример 2.10. Найти интеграл

Решение.

Пример 2.11. Найти интеграл

Решение. Пусть   тогда   

и по формуле интегрирования по частям получаем

=

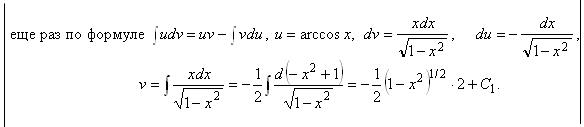
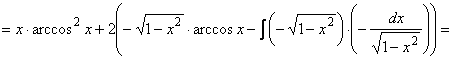
Пример 2.12. Вычислить

Решение. Обозначим

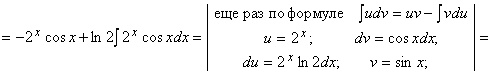
отсюда, выражая I, получим: