Имеет место следующая основная теорема.
Теорема 3.2. Для того чтобы ограниченная на отрезке 
функция 
была интегрируемой на этом отрезке, необходимо и достаточно, чтобы
. (3.3)
Условие (3.3) означает, что для любого 
существует 
такое, что при 
выполняется неравенство 
. Так как 
, то последнее неравенство равносильно неравенству
. (3.4)
Доказательство. Необходимость. Пусть функцияинтегрируема на отрезке, т. е. существует определенный интеграл.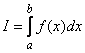 
. Это означает, что для любого существует такое, что для любого разбиения 
, удовлетворяющего
условию независимо от выбора точек 
выполняется неравенство
. (3.5)
Зафиксируем любое такое разбиение . Для него согласно свойству 1о можно указать такие интегральные суммы 
и 
, что
. (3.6)
Отметим, что обе интегральные суммы и удовлетворяют неравенству (3.5). Из соотношения
и неравенств (3.5) и (3.6) следует, что
,
а это и означает выполнения условия (3.4).
Достаточность. Пусть выполнено условие (3.4). Согласно свойству 4о 
для любых нижних и верхних сумм Дарбу, поэтому 
откуда согласно (3.4) следует, что 
для любого . Значит, 
,
т. е.
. Полагая 
, получаем, что для любого разбиения выполняются неравенства
. (3.7)
Если же интегральная сумма 
и суммы Дарбу 
и 
отвечают одному и тому же разбиению, то, как известно,
. (3.8)
Из неравенств (3.7) и (3.8) следует, что
. (3.9)
По условию для любого 
существует 
такое, что при 
выполняется неравенство (3.4): 
. Но тогда из неравенства (3.9) следует, что и
при,
а это означает, что число
является пределом интегральной суммы 
при 
, т. е. функция 
интегрируема на отрезке 
■
Если функция непрерывна на отрезке 
, то она интегрируема на этом отрезке, т.е. предел (3.1) существует и не зависит от способа разбиения промежутка интегрирования на частичные отрезки и от выбора точек 
при каждом таком разбиении.
Основные свойства определенного интеграла
1о.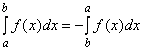 
.
2о.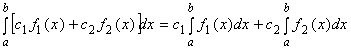 
где 
и 
– постоянные.
3о.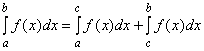 
,
где 
– некоторая точка, лежащая внутри или вне отрезка .