1. Длина дуги гладкой кривой ![]() , содержащейся между двумя точками с абсциссами
, содержащейся между двумя точками с абсциссами ![]() и
и ![]() вычисляется по формуле
вычисляется по формуле
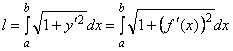 .
.
2. Если кривая задана уравнениями в параметрической форме ![]() ,
,
где ![]() и
и ![]() – непрерывно дифференцируемые функции, то длина дуги кривой будет равна
– непрерывно дифференцируемые функции, то длина дуги кривой будет равна
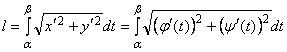 ,
,
где ![]() – значения параметра, соответствующие концам дуги.
– значения параметра, соответствующие концам дуги.
3. Если кривая задана уравнением ![]() в полярной системе координат
в полярной системе координат ![]() , то длина дуги определяется по формуле
, то длина дуги определяется по формуле
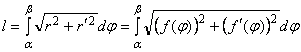 ,
,
где ![]() – значения полярного угла в крайних точках дуги.
– значения полярного угла в крайних точках дуги.
Пример 3.10. Найти длину астроиды ![]() (рис. 3.10).
(рис. 3.10).
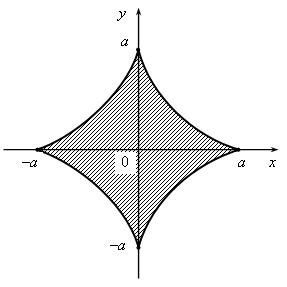
Рис. 3.10. Иллюстрация к примеру 3.10
Решение. Дифференцируем уравнение астроиды, считая, что ![]() :
:
![]() ,
,
откуда
![]() ,
,
поэтому длина дуги одной четвертой части астроиды будет равна

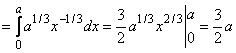 .
.
Отсюда ![]() .
.
Пример 3.11. Найти длину одной арки циклоиды ![]() .
.
Решение. ![]() , следовательно,
, следовательно,
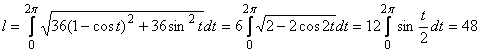 .
.
Пример 3.12. Найти длину кривой ![]() .
.
Решение. ![]() . Длина кривой
. Длина кривой
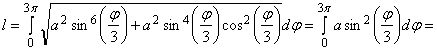
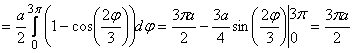 .
.