Теорема 1. Если ![]() f(x) = b, то f(x) = b + a(x), где a(x) – б.м. при x ® a.
f(x) = b, то f(x) = b + a(x), где a(x) – б.м. при x ® a.
Доказательство. Пусть ![]() f (x) = b. Рассмотрим функцию a(x) = f(x) – b и покажем, что a(x) – б.м. при x ® +¥ .
f (x) = b. Рассмотрим функцию a(x) = f(x) – b и покажем, что a(x) – б.м. при x ® +¥ .
Из определения ![]() f (x) = b имеем, что "e > 0 $x0 "x > x0 |f (x) – b| < e, но так как a(x) = f(x) – b, то "e > 0 $x0 "x > x0 |a (x)| < e , а это означает, что a(x) – б.м. при x ® +¥.
f (x) = b имеем, что "e > 0 $x0 "x > x0 |f (x) – b| < e, но так как a(x) = f(x) – b, то "e > 0 $x0 "x > x0 |a (x)| < e , а это означает, что a(x) – б.м. при x ® +¥.
Итак, из равенства a(x) = f(x) – b имеем f(x) = b + a(x), где a(x) – б.м. при x ® +¥.
Теорема 2. Если функцию f(x) можно представить в виде: f (x) = b + a(x), где b – число, a(x) – б.м. функция при x ® a, то ![]() f(x) = b.
f(x) = b.
Доказательство. Пусть f(x) = b + a(x), где a(x) – б.м. при x ® +¥, т.е.
"e > 0 $x0 "x > x0 |a(x)| < e. (*)
Но a(x) = f (x) – b, поэтому (*) можно записать так: "e > 0 $x0 "x > x0 |f (x) – b| < e, что означает: ![]() f (x) = b.
f (x) = b.
Следующие теоремы значительно облегчают нахождение пределов.
Теорема 3. Предел суммы (разности) двух функций равен сумме (разности) их пределов, т.е. если
![]() f1(x) = b1,
f1(x) = b1, ![]() f2(x) = b2, то
f2(x) = b2, то ![]() (f1(x) + f2(x)) = b1 + b2,
(f1(x) + f2(x)) = b1 + b2, ![]() (f1(x) – f2(x) ) = b1 – b2.
(f1(x) – f2(x) ) = b1 – b2.
Доказательство. На основании теоремы 1: f1(x) = b1 + a1(x), f2(x) = b2 + a2(x), где a1(x), a2(x) – б.м. при x ® a, тогда
f1(x) + f2(x) = (b1 + a1(x)) + (b2 + a2(x)) = (b1 + b2) + (a1(x) + a2(x)).
Но a1(x) + a2(x) – б.м. функция при x ® a (как сумма двух б.м. функций), поэтому из равенства f1(x) + f2(x) = (b1 + b2) + (a1(x) + a2(x)) по теореме 2 следует, что
![]()
![]() (f1(x) + f2(x)) = b1 + b2.
(f1(x) + f2(x)) = b1 + b2.
Аналогично проводится доказательство для разности.
Теорема 4. Предел произведения двух функций равен произведению их пределов, т.е. если ![]() f1(x) = b1,
f1(x) = b1, ![]() f2(x) = b2, то
f2(x) = b2, то ![]() (f1(x) f2(x)) = b1× b2.
(f1(x) f2(x)) = b1× b2.
Доказательство. По теореме 1: f1(x) = b1 + a1(x), f2(x) = b2 + a2(x), где a1(x), a2(x) – б.м. при x ® a, тогда f1(x)× f2(x) = b1× b2 + b1×a2(x) + b2×a1(x) + a1(x)× a2(x).
На основании следствий 2, 3, теоремы 1 (разд. 1.6) функции b1×a2(x), b2×a1(x), a1(x)×a2(x) – б.м. при x ® a и a(x) = b1×a2(x) + b2×a1(x) + a1(x)×a2(x) – бесконечно малая функция при x ® a. Из равенства f1(x) f2(x) = b1b2 + a(x) по теореме 2 следует, что ![]() (f1(x)f2(x)) = b1b2.
(f1(x)f2(x)) = b1b2.
Следствие 1. Постоянный множитель можно выносить за знак предела, т.е. ![]() (С×f(x)) = С
(С×f(x)) = С![]() f(x), где С – постоянное число.
f(x), где С – постоянное число.
Доказательство. ![]() С f(x) =
С f(x) = ![]() С
С ![]() f(x) = С
f(x) = С ![]() f(x), так как
f(x), так как ![]() С = С.
С = С.
Следствие 2. Если n – натуральное число, то ![]() [(f(x))n] = (
[(f(x))n] = (![]() f(x))n.
f(x))n.
Теорема 5. Предел дроби равен пределу числителя, деленному на предел знаменателя при условии, что предел знаменателя не равен нулю. Иначе, если ![]() f1(x) = b1,
f1(x) = b1, ![]() f2(x) = b2 и b2 ¹ 0, то
f2(x) = b2 и b2 ¹ 0, то 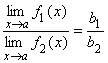 .
.
Доказательство. По теореме 1: f1(x) = b1 + a1(x), f2(x) = b2 + a2(x), где a1(x), a2(x) – б.м. при x ® a, тогда
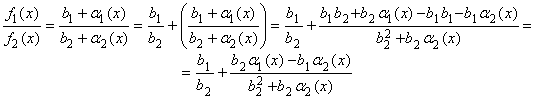
Обозначим последнюю дробь a(x) = 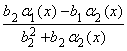 , тогда
, тогда ![]() + a(x). Остается показать, что a(x) – б.м. при x ® a. Действительно, числитель дроби b2a1(x) – b1a2(x) – б.м. по свойствам бесконечно малых функций, предел
+ a(x). Остается показать, что a(x) – б.м. при x ® a. Действительно, числитель дроби b2a1(x) – b1a2(x) – б.м. по свойствам бесконечно малых функций, предел ![]() (b22 + b2a2(x)) = b22 ¹ 0, на основании теорем 3, 4. Поэтому
(b22 + b2a2(x)) = b22 ¹ 0, на основании теорем 3, 4. Поэтому ![]() – функция,ограниченная при x ® a (по теореме 3 разд. 1.6). Значит, a(x) – б.м. при x ® a (по теореме 4 разд. 1.6). Теорема доказана.
– функция,ограниченная при x ® a (по теореме 3 разд. 1.6). Значит, a(x) – б.м. при x ® a (по теореме 4 разд. 1.6). Теорема доказана.
Рассмотрим применение доказанных теорем при нахождении пределов.
Пример. Найти ![]() .
.
Решение. Найдем сначала предел числителя и знаменателя. По свойствам пределов![]() 3 x = 3
3 x = 3![]() x = 3(–2) = –6,
x = 3(–2) = –6, ![]() 1 = 1, поэтому
1 = 1, поэтому ![]() (3x – 1) = –6 – 1 = –7. Аналогично,
(3x – 1) = –6 – 1 = –7. Аналогично, ![]() (5 – 4x) = 5 – 4(–2) = 13. Используя теорему 5, получим:
(5 – 4x) = 5 – 4(–2) = 13. Используя теорему 5, получим:
![]()
![]() .
.
Теорема 6. Если ![]() f(x) существует и f(x) ³ 0 для всех x из области определения функции, то
f(x) существует и f(x) ³ 0 для всех x из области определения функции, то ![]() f(x) ³ 0.
f(x) ³ 0.
Доказательство. Пусть ![]() . Докажем методом от противного, предполагая, что
. Докажем методом от противного, предполагая, что ![]() f(x) = b< 0. Зафиксируем e = –
f(x) = b< 0. Зафиксируем e = –![]() , e > 0. По определению предела по e найдется x0, такое, что "x > x0 |f(x) – b| < e, отсюда b – e < f (x) < b + e. Но e = –
, e > 0. По определению предела по e найдется x0, такое, что "x > x0 |f(x) – b| < e, отсюда b – e < f (x) < b + e. Но e = –![]() , поэтому "x > x0 f(x) < b –
, поэтому "x > x0 f(x) < b –![]() , f(x) <
, f(x) < ![]() , т.е. f(x) < 0, что противоречит условию. Теорема доказана.
, т.е. f(x) < 0, что противоречит условию. Теорема доказана.
Теорема 7. Если "x (f1(x) ³ f2(x)) и ![]() f1(x),
f1(x), ![]() f2(x) существуют, то
f2(x) существуют, то ![]() f1(x) ³
f1(x) ³ ![]() f2(x).
f2(x).
Доказательство. Рассмотрим функцию F(x) = f1(x) – f2(x), тогда "x (F (x) ³ 0) и![]() F(x) существует. По теореме 6:
F(x) существует. По теореме 6: ![]() F(x) ³ 0,
F(x) ³ 0, ![]() (f1(x) – f2(x)) ³ 0, отсюда
(f1(x) – f2(x)) ³ 0, отсюда ![]() f1(x) ³
f1(x) ³ ![]() f2(x). Теорема доказана.
f2(x). Теорема доказана.
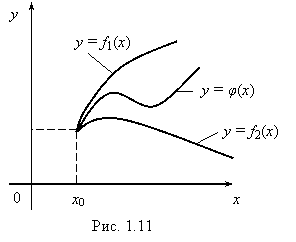
Теорема 8. (теорема о сжатой переменной). Если "x (f1(x) £ j(x) £ f2(x)) и ![]() f1(x) =
f1(x) = ![]() f2(x) = b, то
f2(x) = b, то ![]() j (x) существует и равен b.
j (x) существует и равен b.
 Доказательство
Доказательство
Пусть ![]() f1(x) =
f1(x) = ![]() f2(x) = b (рис. 1.11).
f2(x) = b (рис. 1.11).
Покажем, что ![]() j(x) = b. Зафиксируем e > 0, тогда найдется такое d1 > 0, что
j(x) = b. Зафиксируем e > 0, тогда найдется такое d1 > 0, что
"xÎ(x0, x0 + d1) |f1(x) – b| < e,
и найдется такое d2 > 0, что
"xÎ(x0, x0 + d2) |f2 (x) – b| < e.
Обозначим через d меньшее из d1, d2, тогда для xÎ(x0, x0 + d) эти неравенства будут выполняться одновременно. Преобразуем их, используя определение модуля:
"xÎ(x0, x0 + d) (b – e < f1(x) < b + e),
"xÎ(x0, x0 + d) (b – e < f2(x) < b + e).
И учтем данное неравенство:
f1(x) £ j(x) £ f2(x).
Тогда из этих неравенств получим: b – e < f1(x) £ j(x) £ f2(x) < b + e, откуда b – e < j(x) < b + e или "xÎ(x0, x0 + d) (|j(x) – b| < e), по определению это означает, что ![]() j(x) = b, что и требовалось доказать.
j(x) = b, что и требовалось доказать.