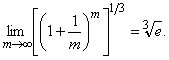Ранее рассматривались понятия последовательности (как функции натурального аргумента), предела последовательности (см. разд. 1.3, 1.4).
Рассмотрим возрастающую последовательность: 
Для нее 
для любого натурального n. Если эта последовательность не является ограниченной, то она не имеет предела, так как ее члены неограниченно возрастают. Если же возрастающая последовательность ограничена, то она имеет предел. Этот факт доказывается в полных курсах математического анализа [6], мы приведем лишь его полную формулировку.
Теорема 1 (достаточный признак существования предела последовательности)
Всякая возрастающая ограниченная сверху последовательность имеет предел.
Применим эту теорему для доказательства следующей теоремы.
Теорема 2 (второй замечательный предел)
Существует предел 
.
Доказательство. Рассмотрим последовательность 
с общим членом 
Покажем, что эта последовательность возрастающая и ограниченная. Для этого воспользуемся формулой бинома Ньютона:
.
Преобразуем по этой формуле 
, полагая 
:
.
В полученном выражении:
третье слагаемое 
четвертое 
=
и т.д., а последнее 
Получаем:
(*)
Покажем, что последовательность 
возрастающая, т.е. 
:
(**)
Так как 
то 
и т.д., поэтому каждое слагаемое (начиная с третьего) из равенства (*) меньше соответствующего слагаемого из равенства (**), кроме того, в равенстве (**) правая часть содержит на одно (положительное) слагаемое больше. Отсюда заключаем, что 
.
Покажем, что последовательность ограничена (сверху), т.е. 
Если в равенстве (**) каждую из скобок 
заменить на 1 (на большее число), то получим неравенство:
Так как 
то
.
По формуле суммы геометрической прогрессии имеем:
поэтому 
.
Последовательность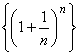 
возрастает и ограничена сверху, по теореме 1 существует предел, этот предел называют неперовым числом и обозначают через e. Итак,
.
Так как 2 < an < 3, то 2 < 
an 
3, т.е. 2 < e 3. Это число e иррациональное и e 
2,718282.
Число e широко используется как основание для показательной функции 
(экспонента) и как основание для логарифмов 
(натуральные логарифмы).
Рассмотрим (рис. 1.13) функцию y = 
, которая не определена на отрезке 
(подумайте почему?). Ее область определения (–
, –1)
(0, +).
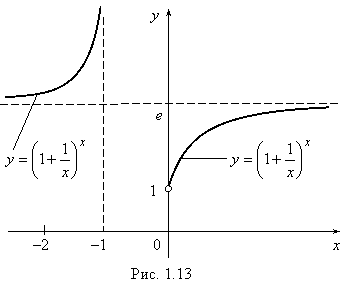Известно, что
и 
.
Нетрудно показать, что
.
Все записанные пределы объединяются одним названием второго замечательного предела.
Рассмотрим применение второго замечательного предела для вычисления некоторых пределов.
Пример. Найти 
Решение. Обозначим: 3n = m, n = 
. Если n
, то m
и мы получим:
= 
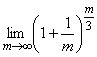