Искусственных источников достаточно, как было указано выше, много. Здесь мы остановимся на рассмотрении только некоторых из этих источников, таких как: токопроводы постоянного и переменного тока и токоограничивающие реакторы.

Токопроводом называется устройство, состоящее из проводников различного профиля и сечения, со всеми относящимися к ним изоляторами, защитными оболочками, ответвительными устройствами, поддерживающими и опорными конструкциями. В зависимости от вида проводников токопроводы подразделяются на гибкие (при использовании проводов) и жесткие (при использовании жестких шин различного профиля и сечения). Токопроводы с фазами, расположенными по вершинам равностороннего треугольника, называются симметричными. Токопроводы применяют для соединения между собой электрических машин и аппаратов распределительных устройств, электрических станций и других предприятий.

Для соединения мощных генераторов с повышающими трансформаторами на блочных станциях широко применяют пофазно-экранированные токопроводы, каждая фаза которых состоит из трубчатой шины, прикрепленной изоляторами к алюминиевому экрану (кожуху). Эти токопроводы изготавливают на заводах и комплектно поставляют на место установки. Токопроводы, выходящие за пределы одной электроустановки, называются протяженными или магистральными.

Токопроводы могут прокладываться либо в закрытых галереях, либо подвешиваться на железобетонных и стальных опорах.

Длительно допустимые токи в токопроводах могут достигать довольно больших значений. Так, токопровод генераторного напряжения (U_н = 24 кВ) типа ТПЭЕ – 24/24000 имеет номинальный ток I_н = 24 кА, а токопровод аппаратно-генераторного комплекса Саяно-Шушенской ГЭС имеет ток I_н = 30 кА. Отсюда видно, что напряжение токопроводов существенно меньше, чем в высоковольтных линиях, однако токи гораздо больше, поэтому они создают более значительное магнитное поле.

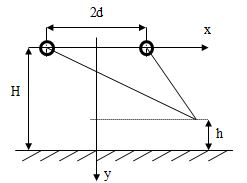
Рис. 3.9. Токопровод постоянного тока

Так, если взять токопровод постоянного тока с номинальным током 30 кА, расстоянием между шинами 2d = 2 м и высотой подвеса проводов Н = 8 м (рис. 3.9), то используя выражения, приведенные в примере 3.2 подраздела 3.1. Можно получить распределение напряженности поля вдоль оси ох на расстоянии h = 1.8 м от земли, показанное на рис. 3.10. Как видно из рисунка, значение напряженности магнитного поля не очень высоко и находится (как будет показано ниже) на уровне допустимых. Однако следует отметить и то обстоятельство, что значения напряженности поля от этого источника на уровне человеческого роста все таки превосходят уровень напряженности поля Земли. Более того, в случае производства ремонтных работ под напряжением, когда обслуживающий персонал находится в непосредственной близости от шин токопровода, напряженность магнитного поля в зоне производства работ может достигать существенных значений. Для иллюстрации этого на рис. 3.11 представлено распределение модуля напряженности поля вдоль оси у под одним из проводов (х = d). Как видно из рисунка, напряженность поля на расстоянии 1 м от оси провода достигает 5 кА/м, а в непосредственной близости от провода – 8 – 9 кА/м.

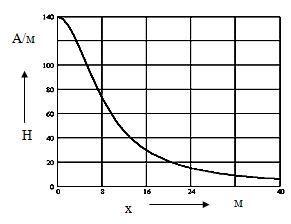
Рис. 3.10. Распределение напряженности поля вдоль оси ох

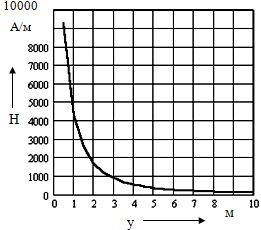
Рис. 3.11. Распределение подуля напряженности поля вдоль оси оу

Рассмотрим теперь магнитное поле под токопроводом трехфазного переменного тока промышленной частоты. Пусть расстояние между осями фаз токопровода равно 3 м, а фазы расположены по вершинам правильного треугольника рис. 3.12. Токопровод выполнен без экранирующих устройств и несет токовую нагрузку, равную 30 кА. Расстояние от нижней фазы до поверхности земли равно 8 м.

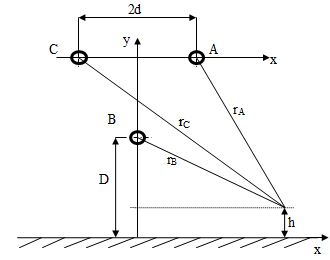
Рис. 3.12. Расположение фаз по вершинам правильного треугольника

В данном случае также удобно использовать формулу, записанную в терминах векторного потенциала, но в комплексной форме. Для каждой фазы комплексное значение векторного потенциала в произвольной точке вне провода определяется с точностью до постоянной следующим выражением:

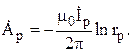
Здесь р – индекс фазы (р = А, В, С); – комплексное значение тока соответствующей фазы; – расстояние от оси фазы до точки, в которой определяется комплексное значение векторного потенциала.

Суммарное значение векторного потенциала от токов во всех трех фазах в этой точке, таким образом, будет равно:

,

где  – фазосдвигающий множитель.

Перепишем выражение для векторного потенциала в прямоугольной системе координат:

,

где .

Учитывая, что векторный потенциал имеет одну составляющую, направленную вдоль оси oz, получим выражения для составляющих напряженности магнитного поля:

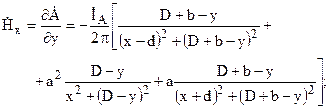
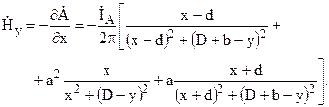
Модуль напряженности магнитного поля, таким образом, определяется при помощи следующего выражения:

.

Графики изменения модулей составляющих напряженности поля и самой напряженности магнитного поля на высоте y = h = 1.8 м вдоль оси ох представлены на рис. 3.13.

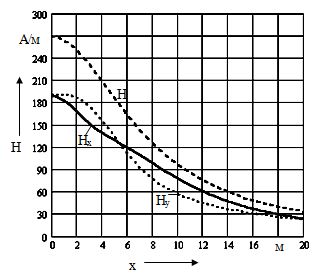
Рис. 3.13. Графики изменения модулей составляющих напряженностей поля

Из графика видно, что максимального значения, равного 270 А/м, модуль напряженности магнитного поля достигает под средней фазой токопровода. Здесь же принимают максимальное значение и модули горизонтальной и вертикальной составляющих напряженности магнитного поля. Причем в этом случае их значения сопоставимы не только с величиной напряженности магнитного поля Земли, но и с допустимыми значениями. При производстве ремонтных работ в непосредственной близости от токопровода персонал может оказаться в зоне достаточно больших магнитных полей. Так, если рассматривать изменение напряженности магнитного поля под крайней фазой вдоль оси оу (рис. 3.14), то можно отметить, что на высоте подвеса средней фазы (у = 8 м) напряженность поля достигает величины, равной 2400 А/м, а при приближении к шине крайней фазы ее значение резко возрастает и может достигать очень больших значений.

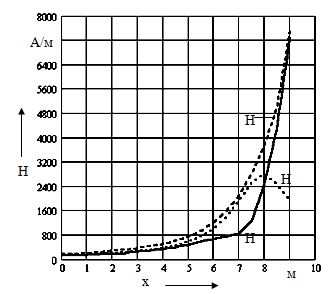
Рис. 3.14. Изменение напряженности магнитного поля под крайней фазой вдоль оси оу

Рассмотрим еще один источник магнитного поля – токоограничивающий реактор. Реакторы служат для ограничения ударного тока короткого замыкания в мощных сетях. Их устанавливают на отходящих фидерах и между секциями сборных шин. Кроме ограничения тока короткого замыкания реакторы одновременно обеспечивают во время короткого замыкания поддержания напряжения на питающих шинах на некотором определенном уровне.

Реактор представляет собой индуктивную катушку без стального сердечника с относительно небольшим активным сопротивлением.

На напряжение до 35 кВ и для внутренней установки (в настоящее время, благодаря высокому качеству изоляции, и для наружной установки) почти исключительное распространение получили бетонные реакторы. Бетонный реактор выполняется в виде концентрически расположенных витков из специального круглого изолированного многожильного провода, залитого в радиально расположенные бетонные колонки.

Обмотки реактора на большие токи выполняются из нескольких параллельных проводов с транспозицией этих параллелей, обеспечивающих равномерное распространение токов. Фазы реактора могут быть расположены горизонтально, вертикально или ступенчато. Все металлические детали реактора выполняются из немагнитных материалов. При больших токах применяется искусственное охлаждение.

Около реакторов создается значительное магнитное поле, которое может оказывать негативное воздействие на обслуживающий персонал и окружающую среду.

Для примера рассмотрим расчет внешнего поля реактора типа РБА-6-2000-12. Это бетонный реактор с алюминиевыми обмотками на напряжение 6 кВ и номинальный ток 2000 А.

Реактор имеет горизонтальное расположение. Обмотка такого реактора выполняется в виде многослойной цилиндрической катушки. Пусть в горизонтальном ряду расположено 8 витков (рис. 3.15), а всего рядов 18. Пусть также обмотка имеет 4 параллельных провода. Расстояние между витками в одном ряду – 0.035 м, а расстояние между рядами – 0.045 м. Средний диаметр обмотки D = 1.195 м. Реактор расположен над поверхностью земли на высоте (расстояние до нижнего витка) h = 0.685 м. Расстояние между осями фаз реактора S = 1.74 м.

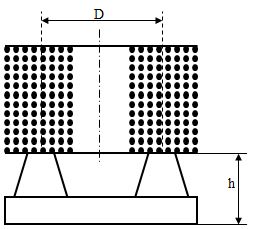
Рис. 3.15. В горизонтальном ряду расположено 8 витков

Для расчета магнитного поля такого реактора вначале рассмотрим расчет поля одного витка, по которому протекает ток i (рис. 3.16). Расчет удобнее проводить при записи уравнения поля в терминах векторного потенциала, поскольку в этом случае можно воспользоваться преобразованной формулой (3.8):

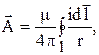
Напомним, что данную формулу можно использовать для расчета поля в точках, отстоящих от проводника на расстояниях, значительно превышающих поперечное сечение самого проводника.

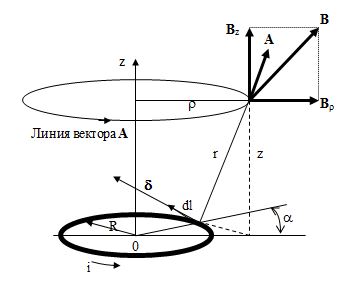
Рис. 3.16. Расчет поля одного витка, по которому протекает ток

Интегрирование по данной формуле производится вдоль всего контура с током. Вследствие симметрии относительно оси 0Z линии векторного потенциала являются окружностями, лежащими в плоскостях, параллельных плоскости контура тока, и имеющими центры на оси 0Z. Таким образом, векторный потенциал имеет единственную составляющую А_a, которая определяется при помощи следующего выражения:

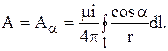
Так как расстояние r от элемента контура с током dl = Rda определяется при помощи формулы:

,

то выражение для векторного потенциала можно переписать в следующем виде:

                                    (3.14)

Интеграл в данном выражении можно привести к эллиптическим интегралам. Для этого положим a = p – 2b; da = -2db; 4Rr/(z² + (R + r)²) = k².

Число k в нашем случае лежит в пределах 0 £ k < 1 (векторный потенциал определяем на достаточном расстоянии от оси проводника с током). Таким образом, имеем cos(a) = = -cos(2b) = 2sin²(b) – 1:

  Следовательно,

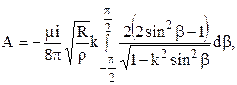
или

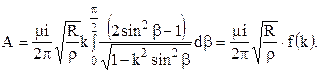
Используя соотношение

можно написать:

где

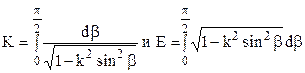
представляют собой полные эллиптические интегралы первого и второго рода, для которых имеются таблицы [103]. Эти интегралы можно аппроксимировать с достаточной точностью многочленами [103]:

,

где а₀ = 1.3862944, а₁ = 0.1119723, а₂ = 0.0725296, b₀ = 0.5, b₁ = 0.1213478, b₂ = 0.0288729, k₁ = 1 – k;

,

где c₁ = 0.4630151, c₂ = 0.1077812, d₁ = 0.2452727, d₂ = 0.0412496.

После определения векторного потенциала с помощью выражения (3.5) находим значения составляющих магнитной индукции:

                                                                            (3.15)

Поскольку реактор имеет множество витков, то для упрощения расчета будем считать, что все витки одного ряда имеют один и тот же диаметр, равный среднему диаметру реактора D. Понятно, что в этом случае следует (для сохранения неизменного значения намагничивающей силы) увеличить величину тока. В нашем случае ток необходимо увеличить в два раза, то есть взять ток, равным 4000 А. Кроме этого, выражение (3.14) удобнее (для учета в последующем фазового сдвига в токах отдельных фаз) представлять в комплексной форме:

.

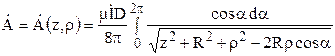Здесь  – комплексное значение тока в витке.

Суммируя затем значения векторных потенциалов от токов в витках, расположенных в разных рядах, получаем общее значение векторного потенциала для одной фазы (например, фазы А) в произвольной точке (z, r):

,

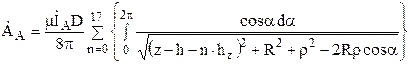где h_z – расстояние между рядами (h_z = 0.045 м).

Используя затем формулы (3.15), находим комплексные значения составляющих напряженности магнитного поля для фазы А:

                                                       (3.16)

Для того чтобы получить общее магнитное поле от трехфазной группы реакторов, необходимо учитывать не только сдвиг по фазе токов, протекающих по обмоткам, но и  взаимное расположение этих обмоток. Например, при горизонтальном расположении фаз реактора так, как показано на рис. 3.17, магнитное поле будет  иметь разное значение в точках, лежащих в торцевой области (линия CD), и в точках, лежащих на оси симметрии группы (линия АВ).

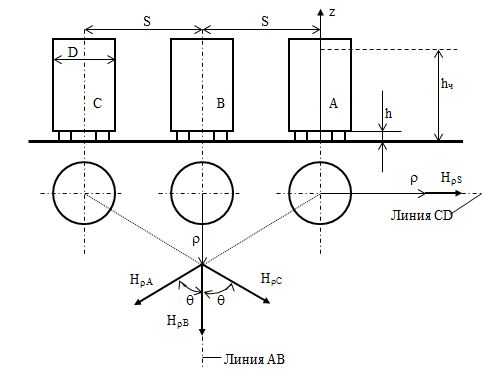
Рис. 3.17. Горизонтальное расположение фаз реактора

Рассмотрим вначале расчет поля для линии АВ (при z = h_ч). Здесь для каждой фазы векторный потенциал будет определяться при помощи следующих формул:

,

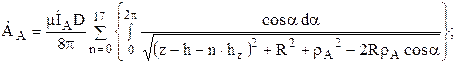
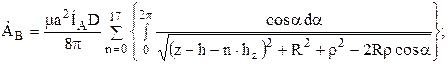
где   – расстояние от оси фазы А и С до точки, в которой определяется потенциал; а – фазосдвигающий множитель; R = D/2.

После расчета векторных потенциалов с помощью выражения (3.16) определяются комплексные составляющие напряженности поля для каждой фазы отдельно, а затем находится их геометрическая сумма:

 .

Здесь q = arctg(S/r).

Общая составляющая напряженности магнитного поля определяется следующим образом:

.

На графике, представленном на рис. 3.18, показано распределение модулей вертикальной H_z и радиальной H_r составляющих напряженности магнитного поля и общей напряженности поля H_S в зависимости от расстояния, отсчитываемого от оси реактора фазы В (см. рис. 3.17) на уровне, соответствующем высоте роста человека (z = 1.8 м).

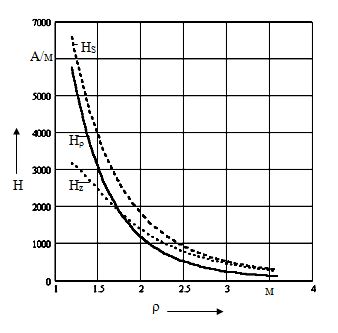
Рис. 3.18. Распределение модулей вертикальной и радиальной составляющих напряженности магнитного поля

Как видно из графиков, общая составляющая напряженности магнитного поля достигает максимального значения, равного 6580 А/м, около обмотки реактора (при r = 1.2 м), а затем она быстро уменьшается и на расстоянии, равном 3 м от оси реактора, принимает значение 400 А/м.

Рассмотрим теперь расчет поля для линии CD (при z = h_ч). Здесь для каждой фазы векторный потенциал будет определяться при помощи следующих формул:

;

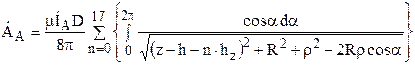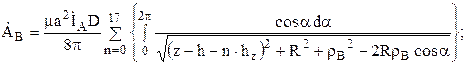
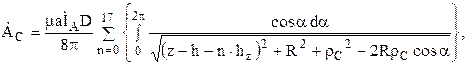
где r_В = r + S – расстояние от оси фазы В до точки, в которой определяется потенциал; r_С = r + 2S – расстояние от оси фазы С до этой же точки.

После расчета векторных потенциалов, также как и в предыдущем случае, определяются комплексные составляющие напряженности поля для каждой фазы отдельно и общая составляющая:

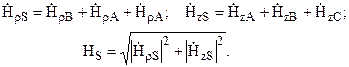
Распределение модулей этих составляющих вдоль линии CD в зависимости от расстояния, отсчитываемого от оси фазы А, также на высоте роста человека (z = 1.8 м) показано на рис. 3.19.

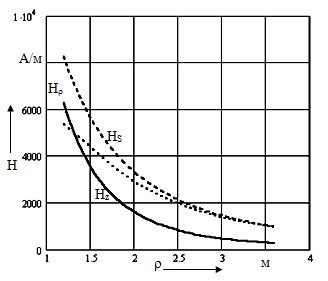
Рис. 3.19. Распределение модулей этих составляющих вдоль линии CD в зависимости от расстояния, отсчитываемого от оси фазы А

Как видно из рисунка, общая составляющая напряженности магнитного поля в данном случае достигает более высокого максимального значения, равного 8250 А/м также на расстоянии r = 1.2 м от оси обмотки (фазы А) реактора. Более того, напряженность поля уменьшается с увеличением расстояния от оси крайней обмотки медленнее и на расстоянии, равном 3 м, она остается достаточно высокой, равной 1500 А/м.