Задержки в элементах логической схемы и межсоединениях ограничивают быстродействие схемы и могут явиться причиной появления сбоя. Различают статические и динамические риски сбоя.
Статический риск сбоя возникает, когда состояние выхода по логике работы схемы должно оставаться неизменным, но происходит его кратковременные изменения (рис. 5.14, 5.15).


Кратковременное изменение состояния выхода типа 1-0-1 называется статическим единичным риском сбоя, кратковременное изменение состояния выхода типа 0-1-0 – статическим нулевым риском сбоя. Возможность появления в проектируемой схеме ложных переходов типа 1-0-1 или 0-1-0 может быть обнаружена на этапе минимизации логической функции.
Пример 5.1. Функция Y = f(A, B, C) задана на карте Карно (рис. 5.16, а). Спроектировать схему, реализующую функцию Y.

Рис. 5.16. Обнаружение статического нулевого риска сбоя: а – минимизация логической функции; б – реализуемая логическая схема; в – временные диаграммы
Решение:
Выполнив склеивание указанных на карте ячеек, получим функцию y в форме МКНФ.
![]() . (5.1)
. (5.1)
Из анализа выражения (5.1) видим, что если В = С=0, то![]() . Выражение
. Выражение ![]() является условием появления в схеме нулевого риска сбоя, что подтверждается временной диаграммой работы (рис. 5.16, в) синтезированной логической схемы (рис. 5.16, б), реализующей логическую функцию (5.1).
является условием появления в схеме нулевого риска сбоя, что подтверждается временной диаграммой работы (рис. 5.16, в) синтезированной логической схемы (рис. 5.16, б), реализующей логическую функцию (5.1).
Чтобы спроектировать логическую схему, гарантированную от появления в ней статического нулевого риска сбоя, необходимо при минимизации исходной функции склеивать все соседние группы ячеек, как это показано на рис. 5.17, а. В результате появляется дополнительный сомножитель (ВÚС) в ранее полученной МДНФ вида (5.1), что не приводит к изменению значения функции, но гарантирует от появления нулевого риска сбоя. Действительно, при В = С = 0 получим:
![]() .
.
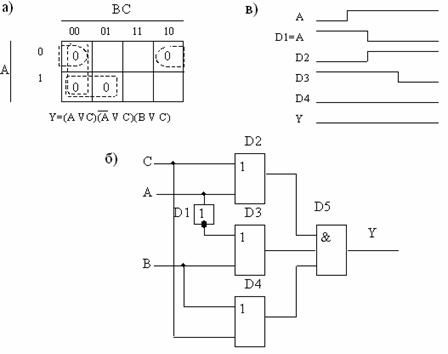
Рис. 5.17. Устранение статического нулевого риска сбоя: а – минимизация логической функции; б – реализуемая логическая схема; в – временные диаграммы
Таким образом, приведенные на рис. 5.17, б, в синтезированная логическая схема и временная диаграмма ее работы иллюстрируют отсутствие нулевого риска сбоя.
Пример 5.2. Функция Y = f(A, B, C) задана на карте Карно (рис. 5.18, а). Спроектировать схему, реализующую функцию Y.
Решение.
Выполнив минимизацию исходной функции, получим МДНФ вида:
![]() . (5.2)
. (5.2)
Подставив в (5.2) значения В=С=1, получим ![]() . Это выражение является условием появления статического единичного риска сбоя. Рис. 5.18, б, в иллюстрирует обнаружение в синтезированной схеме статического единичного риска сбоя.
. Это выражение является условием появления статического единичного риска сбоя. Рис. 5.18, б, в иллюстрирует обнаружение в синтезированной схеме статического единичного риска сбоя.
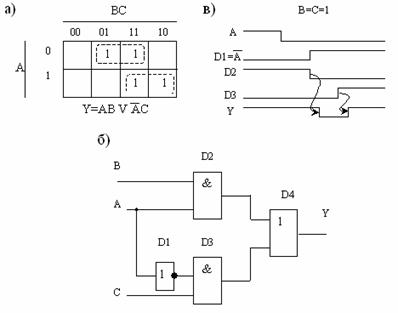
Рис. 5.18. Обнаружение статического единичного риска сбоя: а – минимизация логической функции; б – реализуемая логическая схема; в – временные диаграммы
Для его устранения необходимо провести минимизацию исходной функции, как показано на рис. 5.19, а. В результате получим:
![]() . (5.3)
. (5.3)

Рис. 5.19. Устранение статического единичного риска сбоя: а – минимизация логической функции; б – реализуемая логическая схема; в – временные диаграммы
Логическая схема, реализующая уравнение (5.3), и временная диаграмма ее работы представлены на рис. 5.19, б, в. Анализ работы вновь синтезированной схемы и выражения (5.3) подтверждает устранение единичного риска сбоя. Действительно, при В = С = 1 получаем: ![]() , что свидетельствует об отсутствии единичного риска сбоя.
, что свидетельствует об отсутствии единичного риска сбоя.
Динамический риск сбоя возникает в тех случаях, когда состояние выхода по логике работы схемы должно измениться на противоположное, однако вместо однократного перехода с одного уровня на другой происходят многократные переходы (0-1-0-1 вместо 0-1; 1-0-1-0 вместо 1-0). Такие ситуации могут появиться в схемах, где один какой-либо сигнал проходит по трем и более путям и каждый путь имеет различные задержки распространения сигнала.
Пример 5.3. Проверить есть ли в схеме, изображенной на рис. 5.20, а, динамический риск сбоя.
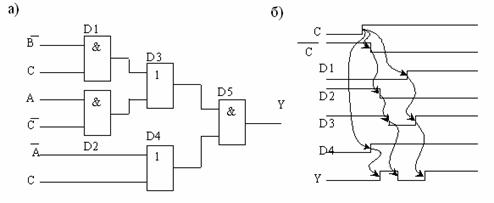
Рис. 5.20. Выявление динамического риска сбоя: а – анализируемая логическая схема; б – временные диаграммы работы схемы
|
Таблица 5.5 Обнаружение динамического риска сбоя |
||
|
ABC |
Изменение С |
Динамический риск |
|
000 001 010 011 100 101 110 111 |
0—1 1—0 0—1 1—0 0—1 1—0 0—1 1—0 |
Нет Нет Нет Нет Да, если tздD1> tздD2 Нет Нет Нет |
Решение.
Так как сигнал С может проходить по трем различным путям, то в схеме возможен динамический риск сбоя. Проведем анализ работы схемы при различных входных воздействиях. Если А = 0 (первые четыре комбинации сигналов в табл. 5.5), то на выходе элемента D4 сигнал равен единице, на выходе D2 сигнал равен нулю, и, следовательно, на выходе D5 динамического риска быть не может. Если В = 1, то D1 = 0 и на выходе D5 не может быть динамического риска. Таким образом, проверка на шести наборах, когда А = 0 или В = 1, показала, что динамические риски сбоя в схеме отсутствуют.
Анализ работы схемы при условии А = 1, В = 0 и при изменении сигналов С из нуля в единицу выявляет динамический риск сбоя на элементе D5 (рис. 5.20, б). На других наборах динамического риска сбоя нет. Для того чтобы построить схему, гарантированную как от статических, так и от динамических рисков сбоя, необходимо при проектировании логической схемы добиваться одинаковых по задержкам путей следования сигналов.