Рассмотрим инструментальную погрешность (ξин). Значение ξин складывается из множества составляющих, причём некоторые из них проявляются случайным образом и распределены по различным законам (погрешность от зазора в кинематической цепи, от трения в опорах), а другие проявляются систематическим образом (погрешность установки нуля). Суммарный закон распределения случайной составляющей инструментальной погрешности (ξин) является, таким образом, композицией различных законов и, как правило, неизвестен экспериментатору при обработке им результатов испытаний.
В паспорте прибора указывается доверительный интервал инструментальной погрешности прибора (Δ) (или, по принятой терминологии, – основная допускаемая погрешность), который устанавливается предприятием-разработчиком, чаще всего экспериментальным путём (сравнением с эталонными и образцовыми приборами).
Значение основной допускаемой погрешности (Δ) гарантируется для нормальных атмосферных условий, например, температуры окружающего воздуха t0 = 20 ± 5 ºС, барометрического давления В0 = (760 ± 25) мм рт. ст. или (101,3 ± 3,3) кПа и т.д. Если рабочие условия эксплуатации прибора отличаются от нормальных, указанных в паспорте, то основная допускаемая погрешность (Δ) возрастает на значение дополнительной погрешности, также указываемой в паспорте прибора. Основная допускаемая погрешность прибора, как правило, согласована с его шкалой – значение Δ не должно быть меньше половины шкалы деления шкалы.
Рассмотрим погрешность (ξпр), обусловленную прочими причинами, складывающуюся из многих составляющих, проявляющихся как случайным, так и систематическим образом:
ξпр = ξсл + ξсист.
Систематическая погрешность (ξсист), как было указано ранее, при проведении повторных изменений остаётся неизменной или изменяется по детерминированному закону и, следовательно, может быть установлена расчётным или экспериментальным путём. После вычисления или опытного определения ξсист она устраняется путём прибавления к результату измерения поправки (γ), равной значению систематической погрешности, взятой с обратным знаком:
γ = – ξсист.
Погрешность ξсл – случайная величина, и для неё справедливы все выводы теории вероятности. Часто при повторных измерениях в эксперименте величина ξсл порождается множеством причин, роль каждой из которых в образовании ξсл невелика. Следовательно, в силу центральной предельной теоремы Ляпунова ξсл распределяется по нормальному закону, симметрично относительно нуля с плотностью вероятности:
![]()
где ![]() – среднеквадратичное отклонение случайной величины;
– среднеквадратичное отклонение случайной величины; ![]() – дисперсия случайной величины.
– дисперсия случайной величины.
Допустим, что систематическая погрешность (ξсист) устранена с помощью введения поправки (γ), а инструментальная погрешность ξин << ξпр, и ею можно пренебречь. Тогда истинная погрешность
ξ = ξсл и х = ξсл + А.
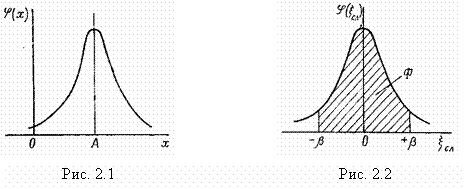
Следовательно, результат измерения х также является случайной величиной, распределённой по нормальному закону (рис. 2.1.) с плотностью вероятности ![]() , симметрично относительно А, где
, симметрично относительно А, где
![]() .
.
Из теории вероятности известно, что, если случайная величина (х) распределена по нормальному закону, то для её выборки (ряда повторных измерений) математическое ожидание (выборочное среднее)
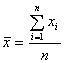 ,
,
где хi- результаты повторных измерений; п – число повторных измерений.
Дисперсия выборки (![]() ) при этом может быть определена по приближённой формуле:
) при этом может быть определена по приближённой формуле:
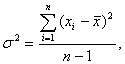
где п – 1 = f – число степеней свободы дисперсии ![]() . При
. При ![]() .
.
Доверительный интервал случайной погрешности отдельного измерения ± β – это диапазон, за пределы которого ξсл не выйдет с заданной вероятностью Р. Вероятность Р (рис. 2.2, заштрихованная площадь) определяется по формуле:
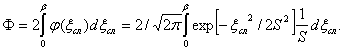
 Обозначим
Обозначим ![]() , тогда
, тогда ![]() . При ξсл = β t = ta = β / S. Получаем интеграл Лапласа:
. При ξсл = β t = ta = β / S. Получаем интеграл Лапласа:
![]()
Величина ta = β / S называется коэффициентом Стьюдента. Значения коэффициента Стьюдента, определённые для различных значений вероятности (Р) из интеграла Лапласа:
|
Р |
0,68 |
0,95 |
0,997 |
0,999 |
0,9999 |
|
ta |
1,0 |
2,0 |
3,0 |
3,5 |
4,0 |
Доверительный интервал случайной погрешности отдельного измерения, таким образом, равен:
β = taS.
На практике для определения доверительного интервала (β) используют выборки, содержащие ограниченное число повторных измерений (п = 2…10). Поэтому β определяют по приближённой формуле:
β = ta 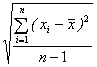 ,
,
где
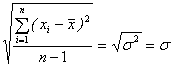
- среднеквадратичная погрешность отдельного измерения выборки.
Для компенсации возникающей ошибки (тем большей, чем меньше п) коэффициент Стьюдента определяют не с помощью интеграла Лапласа, а с помощью интеграла Стьюдента, учитывающего число повторных измерений (табл. 2.1). На практике при определении коэффициента Стьюдента принято задаваться вероятностью Р = 0,95.
С помощью доверительного интервала случайной погрешности отдельного измерения (β) может быть определён доверительный интервал отдельного измерения:
![]() ,
,
где ![]() .
.
Таблица 2.1
|
n |
Р |
|||
|
0,68 |
0,95 |
0,997 |
0,999 |
|
|
2 3 4 5 6 7 8 9 10 |
2,0 1,3 1,3 1,2 1,2 1,1 1,1 1,1 1,1 |
12,7 4,3 3,2 2,8 2,6 2,4 2,4 2,3 2,3 |
31,8 7,0 4,5 3,7 3,4 3,1 3,0 2,9 2,8 |
636,0 31,6 12,9 8,6 6,9 6,0 5,4 5,0 4,8 |
Доверительный интервал отдельного измерения (![]() ) позволяет утверждать, что результат любого повторного измерения должен находиться в границах:
) позволяет утверждать, что результат любого повторного измерения должен находиться в границах:
![]()
Определим доверительный интервал (![]() ) в случайной погрешности математического ожидания (
) в случайной погрешности математического ожидания (![]() ). В теории вероятностей доказывается теорема о дисперсии случайной величины(
). В теории вероятностей доказывается теорема о дисперсии случайной величины(![]() ), являющейся функцией нескольких случайных величин
), являющейся функцией нескольких случайных величин
![]() = f (x1, x2,…xn),
= f (x1, x2,…xn),
распределённых по нормальному закону, причём
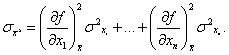
Воспользуемся этой теоремой. Математическое ожидание вычисляется по формуле:
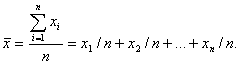
Поскольку х1, х2 …, хп – случайные числа, распределённые по нормальному закону, и дисперсия их равна σ2, то в силу упомянутой теоремы дисперсия математического ожидания равна:
![]()
и среднеквадратичная погрешность математического ожидания определяется по формуле:
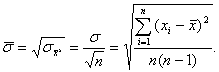
Из последнего выражения следует важный вывод о повышении точности при увеличении числа повторных измерений (п): при росте п среднеквадратичная погрешность математического ожидания (![]() ) уменьшается пропорционально
) уменьшается пропорционально ![]() .
.
Зная ![]() , определяем:
, определяем:
· доверительный интервал случайной погрешности математического ожидания
![]() ;
;
· доверительный интервал математического ожидания
![]()
где ta выбирается по таблице 2.1 в соответствии с числом повторных измерений п для вероятности Р = 0,95.
Для нахождения доверительного интервала (![]() ) мы воспользовались допущением о том, что ξин << ξсл. В общем случае ξин и ξсл могут быть величинами одного порядка. Поскольку закон распределения случайной составляющей ξин, как правило, неизвестен, то для определения доверительного интервала истинной погрешности (а) рекомендуется приближённая формула:
) мы воспользовались допущением о том, что ξин << ξсл. В общем случае ξин и ξсл могут быть величинами одного порядка. Поскольку закон распределения случайной составляющей ξин, как правило, неизвестен, то для определения доверительного интервала истинной погрешности (а) рекомендуется приближённая формула:
![]()
Если ![]() (практически, если
(практически, если ![]() ), то можно полагать
), то можно полагать ![]() Если
Если ![]() , то можно полагать а = Δ и ограничиться однократным измерением.
, то можно полагать а = Δ и ограничиться однократным измерением.