При использовании ортогональных центральных композиционных планов (ОЦКП) можно получить все коэффициенты квадратичных полиномов (см п.3.2.). Планы второго порядка предполагают исследование не в трех точках (+1, -1, 0), а в пяти (-α, -1, 0, +1, + α); здесь ± α – «звездные точки», т.е. диапазон варьирования факторов разбивается на четыре участка.
Соответственно «+α» обозначает максимальное значение фактора; «-α» – минимальное значение фактора; «+1», «0», «-1» – точки внутри диапазона варьирования.
Кодирование факторов производится по формуле (3.1).
Значения «звездного» плеча (α) для разного количества факторов (К) составляют:
|
К |
2 |
3 |
4 |
5 |
|
α |
1,0 |
1,215 |
1,414 |
1,547 |
Для полных планов второго порядка при ином значении К, а также для дробных планов второго порядка значения «звездного» плеча (α) определяется из формулы:
.
Первоначальное преобразование квадратичных членов производится по формуле:
,
где 
– сумма i-го столбца матрицы.
Квадратичный член имеет вид:
.
Подсчет коэффициентов (bi) производится по формуле:
.
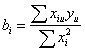Первоначально полином ищется в виде:
.
Для перехода к обычному виду (3.5) осуществляется преобразование свободного члена:
.
В табл. 3.14 дан ОЦКП для трех факторов. Число опытов для ОЦКП второго порядка подсчитывается по формуле:
.
Оценка значимости полученных коэффициентов (bi) производится согласно t-критерию (Стьюдента) по формуле:
, (3.6)
где 
– среднеквадратическое отклонение; 
– дисперсия коэффициентов.
В свою очередь, определяется по формуле:
,
где 
– дисперсия опыта, равная
.
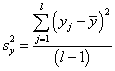Таблица 3.14
|
Элементы плана эксперимента |
|
х0 |
х1 |
х2 |
х3 |
х4’= х12 – 0,73 |
х5 ’= 22 2- 0,73 |
х6 ’= х3 2 -0,73 |
х7 = х1х2 |
х 8= х1х3 |
х9 = х2х3 |
у |
|
План полного факторного эксперимента типа 23 |
1 |
+1 |
-1 |
-1 |
-1 |
0,27 |
0,27 |
0,27 |
+1 |
+1 |
+1 |
у1 |
|
2 |
+1 |
+1 |
-1 |
-1 |
0,27 |
0,27 |
0,27 |
-1 |
-1 |
+1 |
у2 |
|
|
3 |
+1 |
-1 |
+1 |
-1 |
0,27 |
0,27 |
0,27 |
-1 |
+1 |
-1 |
у3 |
|
|
4 |
+1 |
+1 |
+1 |
-1 |
0,27 |
0,27 |
0,27 |
+1 |
-1 |
-1 |
у4 |
|
|
5 |
+1 |
-1 |
-1 |
+1 |
0,27 |
0,27 |
0,27 |
+1 |
-1 |
-1 |
у5 |
|
|
6 |
+1 |
+1 |
-1 |
+1 |
0,27 |
0,27 |
0,27 |
+1 |
+1 |
-1 |
у6 |
|
|
7 |
+1 |
-1 |
+1 |
+1 |
0,27 |
0,27 |
0,27 |
-1 |
-1 |
+1 |
у7 |
|
|
8 |
+1 |
+1 |
+1 |
+1 |
0,27 |
0,27 |
0,27 |
+1 |
+1 |
+1 |
у8 |
|
|
«Звездные» точки |
9 |
+1 |
-1,215 |
0 |
0 |
0,75 |
-0,73 |
-0,73 |
0 |
0 |
0 |
у9 |
|
10 |
+1 |
+1,215 |
0 |
0 |
0,75 |
-0,73 |
-0,73 |
0 |
0 |
0 |
у10 |
|
|
11 |
+1 |
0 |
-1,215 |
0 |
-0,73 |
0,75 |
-0,73 |
0 |
0 |
0 |
у11 |
|
|
12 |
+1 |
0 |
+1,215 |
0 |
-0,73 |
0,75 |
-0,73 |
0 |
0 |
0 |
у12 |
|
|
13 |
+1 |
0 |
0 |
-1,215 |
-0,73 |
-0,73 |
0,75 |
0 |
0 |
0 |
у13 |
|
|
14 |
+1 |
0 |
0 |
+1,215 |
-0,73 |
-0,73 |
0,75 |
0 |
0 |
0 |
у14 |
|
|
Нулевая точка |
15 |
+1 |
0 |
0 |
0 |
-0,73 |
-0,73 |
-0,73 |
0 |
0 |
0 |
у15 |
Здесь l – число параллельных опытов, проводимых в нулевой точке плана; 
- среднее значение 
.
В случае выполнения неравенства (3.6) коэффициент bi считается значимым, в случае невыполнения коэффициент bi считается незначимым и отбрасывается. Далее проверяется неравенство:
, (3.7)
где 
– табличное значение F-критерия; 
– дисперсия адекватности.
Дисперсия адекватности определяется по формуле:
,
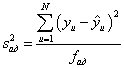где 
– наблюденное (определенное из опыта) значение выходной величины; 
– предсказанное (рассчитанное по полиному) значение выходной величины; 
- число степеней свободы (m – число определяемых коэффициентов bi).
В случае выполнения неравенства (3.7) математическая модель процесса считается адекватной при определенном уровне достоверности.