Как мы уже отметили, задача оптимизации – это задача отыскания таких значений факторов х1 = х1*, х2 = х2*, …, хk = хk*, при которых функция отклика (у) достигает экстремального значения у = ext (оптимума).
Известны различные методы решения задачи оптимизации. Одним из наиболее широко применяемых является метод градиента, называемый также методом Бокса-Уилсона и методом крутого восхождения.
Рассмотрим сущность метода градиента на примере двухфакторной функции отклика y = f(x1, х2). На рис. 4.3 в факторном пространстве изображены кривые равных значений функции отклика (кривые уровня). Точке с координатами х1*, х2* соответствует экстремальное значение функции отклика уext.
Если мы выберем какую-либо точку факторного пространства в качестве исходной (х1 0, х2 0), то наикратчайший путь к вершине функции отклика из этой точки – это путь, по кривой, касательная к которой в каждой точке совпадает с нормалью к кривой уровня, т.е. это путь в направлении градиента функции отклика.
 Градиент непрерывной однозначной функции y = f(x1, х2) – это вектор, определяемый по направлению градиентом с координатами:
Градиент непрерывной однозначной функции y = f(x1, х2) – это вектор, определяемый по направлению градиентом с координатами:
![]()
где i, j – единичные векторы в направлении осей координат х1 и х2. Частные производные ![]() и
и ![]() характеризуют направление вектора.
характеризуют направление вектора.
Поскольку нам неизвестен вид зависимости y = f(x1, х2), мы не можем найти частные производные ![]() ,
, ![]() и определить истинное направление градиента.
и определить истинное направление градиента.
Согласно методу градиента в какой-то части факторного пространства выбирается исходная точка (исходные уровни) х1 0, х2 0. Относительно этих исходных уровней строится симметричный двухуровневый план эксперимента. Причем интервал варьирования выбирается настолько малым, чтобы линейная модель оказалась адекватной. Известно, что любая кривая на достаточно малом участке может быть аппроксимирована линейной моделью.
После построения симметричного двухуровневого плана решается интерполяционная задача, т.е. строится линейная модель:
![]()
и проверяется ее адекватность.
Если для выбранного интервала варьирования линейная модель оказалась адекватной, то может быть определено направление градиента:
![]()
Таким образом, направление градиента функции отклика определяется значениями коэффициентов регрессии. Это означает, что мы будем двигаться в направлении градиента, если из точки с координатами (![]() ) перейдем в точку с координатами:
) перейдем в точку с координатами:
![]() ,
,
где m – положительное число, определяющее величину шага в направлении градиента.
Поскольку х1 0 = 0 и х2 0 = 0, то ![]() .
.
Определив направление градиента (![]() ) и выбрав величину шага m, осуществляем опыт на исходном уровне х1 0, х2 0. Затем делаем шаг в направлении градиента, т.е. осуществляем опыт в точке с координатами
) и выбрав величину шага m, осуществляем опыт на исходном уровне х1 0, х2 0. Затем делаем шаг в направлении градиента, т.е. осуществляем опыт в точке с координатами ![]() . Если значение функции отклика возросло по сравнению с ее значением в исходном уровне, делаем еще шаг в направлении градиента, т.е. осуществляем опыт в точке с координатами:
. Если значение функции отклика возросло по сравнению с ее значением в исходном уровне, делаем еще шаг в направлении градиента, т.е. осуществляем опыт в точке с координатами:
![]() .
.
 Движение по градиенту продолжаем до тех пор, пока функция отклика не начнет уменьшаться. На рис. 4.3 движение по градиенту соответствует прямой, выходящей из точки (х1 0, х2 0). Она постепенно отклоняется от истинного направления градиента, показанного штриховой линией, вследствие нелинейности функции отклика.
Движение по градиенту продолжаем до тех пор, пока функция отклика не начнет уменьшаться. На рис. 4.3 движение по градиенту соответствует прямой, выходящей из точки (х1 0, х2 0). Она постепенно отклоняется от истинного направления градиента, показанного штриховой линией, вследствие нелинейности функции отклика.
Как только в очередном опыте значение функции отклика уменьшилось, движение по градиенту прекращают, принимают опыт с максимальным значением функции отклика за новый исходный уровень, составляют новый симметричный двухуровневый план и снова решают интерполяционную задачу.
Построив новую линейную модель ![]() , осуществляют регрессионный анализ. Если при этом проверка значимости факторов показывает, что хоть один коэф
, осуществляют регрессионный анализ. Если при этом проверка значимости факторов показывает, что хоть один коэф
фициент ![]() , значит, область экстремума функции отклика (область оптимума) еще не достигнута. Определяется новое направление градиента и начинается движение к области оптимума.
, значит, область экстремума функции отклика (область оптимума) еще не достигнута. Определяется новое направление градиента и начинается движение к области оптимума.
Уточнение направления градиента и движение по градиенту продолжаются до тех пор, пока в процессе решения очередной интерполяционной задачи проверка значимости факторов не покажет, что все факторы ![]() незначимы, т.е. все
незначимы, т.е. все ![]() . Это означает, что область оптимума достигнута. На этом решение оптимизационной задачи прекращают, и принимают опыт с максимальным значением функции отклика за оптимум.
. Это означает, что область оптимума достигнута. На этом решение оптимизационной задачи прекращают, и принимают опыт с максимальным значением функции отклика за оптимум.
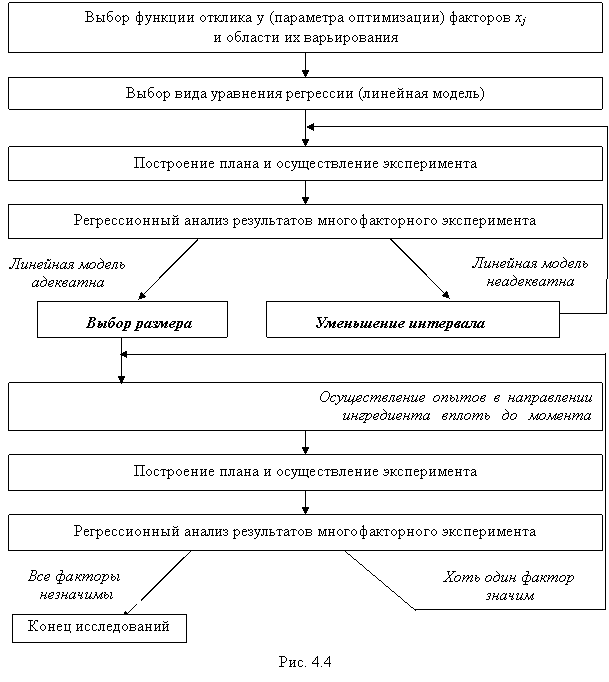
В общем виде последовательность действий, необходимых для решения задачи оптимизации методом градиента, может быть представлена в виде блок-схемы (рис. 4.4).
В заключение приведем некоторые рекомендации выбора исходного уровня, интервалов варьирования и значения шага при решении задачи оптимизации методом градиента:
1) исходные уровни факторов (хj 0) следует выбирать возможно ближе к точке оптимума, если есть какая-то априорная информация о ее положении;
2) интервалы варьирования (Δхj) надо выбирать такими, чтобы линейная модель наверняка оказалась адекватной. Границей снизу Δхj при этом является минимальное значение интервала варьирования, при котором функция отклика остается значимой;
3) значение шага (т) при движении по градиенту выбирают таким образом, чтобы наибольшее из произведений ![]() не превышало разности верхнего и нижнего уровней факторов в нормированном виде
не превышало разности верхнего и нижнего уровней факторов в нормированном виде
![]() .
.
Следовательно, 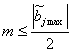 . При меньшем значении т разность функции отклика в исходном уровне и в точке с координатами
. При меньшем значении т разность функции отклика в исходном уровне и в точке с координатами ![]() может оказаться незначимой. При большем значении шага возникает опасность проскочить оптимум функции отклика.
может оказаться незначимой. При большем значении шага возникает опасность проскочить оптимум функции отклика.