Пластическая деформация металла начинается, если численные значения инвариантов тензора-девиатора напряжений, а именно интенсивность касательных напряжений достигнет значений предела текучести при сдвиге:
![]() .
.
Процессы упрочнения и разупрочнения в ходе развития деформации значительно изменяют критические значения пороговых напряжений по сравнению с пределом текучести. Это означает, что каждому моменту времени по ходу пластической деформации соответствуют свои значения ts и ss, определяемые всей предысторией деформации данного конкретного материала. В общем случае сопротивление деформации представляет сложную зависимость от температуры (Т), степени (e) и скорости (x) деформации, закона развития деформации во времени e(t) и физико-механических свойств материала (Х), т.е.
![]() .
.
Сопротивление деформации (ss) может совпадать с tт или sт только в частном случае при очень малой относительной статической деформации образца (e £ 0,001).
В практических расчетах для определения сопротивления деформации металлов и сплавов используют результаты экспериментальных исследований, представленных графическими или аналитическими зависимостями.
При холодной деформации сопротивление деформации монотонно возрастает с повышением степени деформации. Характер этой зависимости приближенно моделируется уравнением:
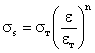 , (3.1)
, (3.1)
где sт – предел текучести материала; eт – условная степень деформации начала пластического течения; e – степень деформации.
Условно начало пластической деформации в расчетах можно принимать eт » 0,002
С повышением температуры процесса сопротивление материала деформированию экспоненциально понижается. Но вблизи температур полиморфных превращений плавный ход температурной зависимости сопротивления деформации может терять свою монотонность. С повышением скорости и степени пластической деформации сопротивление материала, как правило, возрастает, однако для ряда материалов на кривой «ss – e» возможно появление максимума.
Для практических расчетов удобно пользоваться аналитическими зависимостями, аппроксимирующими экспериментальные данные. Наибольшее распространение получила зависимость Андреева-Тюленева /1/:
![]() , (3.2)
, (3.2)
где sо – базовое сопротивление деформации при x =1, e = 0,1 и Т = 1000 оС; k, a, b, c – эмпирические коэффициенты, численные значения которых для некоторых сталей приведены в таблице 3.1.
Таблица 3.1