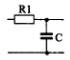
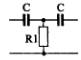
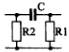
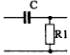
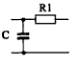
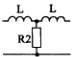
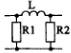
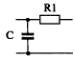
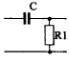
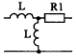
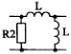
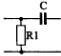
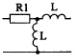
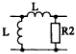
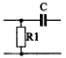
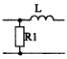
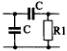
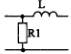
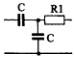
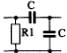
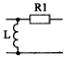
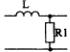
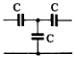
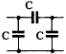
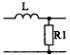
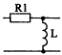
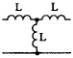
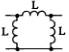
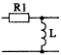
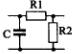
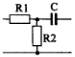
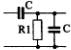
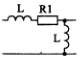
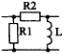
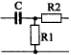
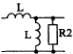
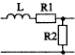
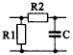
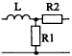
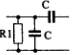
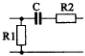
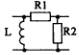
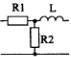
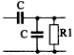
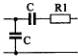
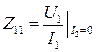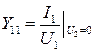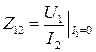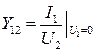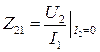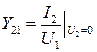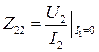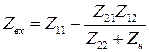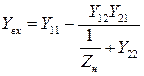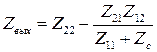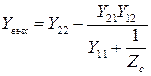1) Номер схемы четырехполюсника равен номеру варианта N. Схемы четырехполюсников приведены в табл. 10.

Таблица 10

N	Схема четырехполюсника		N	Схема четырехполюсника
	Y- параметров	Z-параметров		Y- параметров	Z-параметров
1			13
2			14
3			15
4			16
5			17
6			18
7			19
8			20

Продолжение таблицы 10

9			21
10			22
11			23
12			24

Параметры элементов четырехполюсника даны в табл. 11.

Таблица 11

Задание	L, Гн	C, нФ	R1, кОм	R2, кОм	Rс, кОм	Rн, кОм
1	3N	N	2N	6N	2N	4N
2	200N	150N	N	6N	N	5N
Примечание: задание 1 – для Y- параметров; задание 2 – для Z — параметров

К четырехполюснику подключается источник гармонического напряжения и нагрузка (рис. 59). В табл. 11 указаны: Rс – сопротивление источника сигнала; Rн — сопротивление нагрузки четырехполюсника. Амплитуда напряжения источника U_m выбирается самостоятельно в диапазоне от 1 мВ до 10 В (самостоятельно выбрать 5 — 7 точек).

Расчет провести на частоте: F = 200/N кГц – для Y- параметров;

F = 2/N кГц – для Z-параметров.

2) Используя методы короткого замыкания или холостого хода рассчитать по формулам Y и Z- параметры четырехполюсников.

При анализе удобно рассматривать четырехполюсник в виде «черного ящика», т.е. устройства с некоторой неизвестной внутренней структурой. Внутренняя структура будет проявляться через взаимосвязь входных и выходных токов и напряжений.

Заданы: входной I₁ и выходной I₂ токи четырехполюсника (рис. 59). Входные и выходные напряжения U₁ и U₂ четырехполюсника будут функциями этих токов:

.

Так как четырехполюсник линейный, то в силу принципа суперпозиции, функции, записанные в этих уравнениях, будут линейными:

,

где Z₁₁, Z₁₂, Z₂₁, Z₂₂ – сопротивления, определяемые внутреннюю структуру четырехполюсника, при наличии реактивных элементов эти сопротивления являются комплексными.

Данные уравнения называют уравнениями четырехполюсника с Z-параметрами.

Система уравнений может быть представлена в матричной форме

.

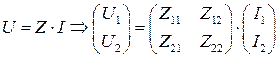Заменяя на рис. 59 источники тока источниками напряжения и используя принцип суперпозиции, можно получить уравнения, связывающие токи и напряжения четырехполюсника

,

где Y₁₁, Y₁₂, Y₂₁, Y₂₂ – проводимости четырехполюсника.

Данные уравнения называют уравнениями четырехполюсника с Y-параметрами.

Из анализа уравнений четырехполюсника можно получить физический смысл параметров четырехполюсников (табл. 12)

Таблица 12

Z-параметры	Значение	Y-параметры	Значение
	Входное сопротивление		Входная проводимость при коротком замыкании на выходе
	Сопротивление обратной связи		Проводимость обратной связи
	Сопротивление прямой передачи		Сопротивление прямой передачи
	Выходное сопротивление при холостом ходе на выходе		Выходная проводимость при коротком замыкании на выходе

Z-параметры называют параметрами холостого хода, Y-параметры – параметрами короткого замыкания. Четырехполюсник используется в системах передачи сигналов. Для анализа прохождения сигналов через четырехполюсник вводятся функции четырехполюсника:

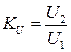 – Комплексный коэффициент передачи по напряжению

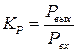– Коэффициент передачи активной мощности

 – Комплексный коэффициент передачи по току

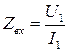 – Комплексное входное сопротивление

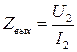 – Комплексное выходное сопротивление

Используя данные параметры, рассчитать:

- комплексный коэффициент передачи;

входное и выходное сопротивления с учетом сопротивлений источника

- сигнала Rс и нагрузки Rн.

Для Z и Y-параметров четырехполюсников данные функции определены выражениями (табл. 13).

Таблица 13

Z-параметры	Y-параметры	Значение
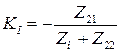
		Комплексный коэффициент передачи
		Входная проводимость четырехполюсника
		Выходное сопротивление четырехполюсника

3) Рассчитать комплексный коэффициент передачи четырехполюсника в широком диапазоне частот и проверить на заданной частоте результаты, полученные аналитически. Допускается погрешность не более 30 %. Построить амплитудно-частотные характеристики.

Включая на входе четырехполюсника последовательно с Rс амперметр и измеряя действующее значение входного тока, определить модуль комплексного входного сопротивления четырехполюсника. Построить зависимость величины входного сопротивления четырехполюсника от амплитуды входного напряжения.

Включая на выходе четырехполюсника последовательно с резистором Rн, амперметр и измеряя действующее значение выходного тока, определить модуль комплексного выходного сопротивления четырехполюсника. Построить соответствующие зависимости.

Эксперименты выполнить в Electronics Workbench.

Полученные экспериментальным путем данные в пояснительной записке РГЗ представить таблично.

Расчеты и построение характеристик реализовать в среде MATHCAD.