1,005
1,026
1,054
1,083
1,151
1,386
1,720
2,558
п) с учетом поправки L рассчитать температуру наружной поверхности медной трубы в «горячей» зоне (q » 72,2 °С).
Ответ:Q=160,4 Вт; q=72,2°С ;q1=31,4·104Вт/м2.
Пример 7. В условиях предыдущей задачи, полагая, что тепловая труба имеет длину L = 150 мм (см. рис. П 5.7), рассчитать ее условный коэффициент теплопроводности и сравнить его с коэффициентом теплопроводности сплошною медного стержня.
Алгоритм расчета и комментарии к нему:
а) полагая, что труба представляет собой сплошной стержень; определить средний градиент температуры между ее торцами [gradQ»(72-20)/0,15=347oC/м];
б) рассчитать условный коэффициент теплопроводности трубы l Т = 36 Вт/(м·°С).;
в) определить, во сколько раз условный коэффициент теплопроводности тепловой трубы превышает коэффициент теплопроводности сплошного медного стержня.
Ответ: примерно в 2,5 раза.
15. Алюминиевая заготовка имеет после полирования температуру поверхности 100°С. Определить плотность теплового потока, который эта заготовка излучает в окружающую среду. Ответ: Е = 55 Вт/м2.
Пример 8. Встроенный электродвигатель 1 мощностью 3 кВт размещен в стойке станка 2 (рис. П5.8). Внутренняя часть стойки и поверхность двигателя окрашены масляной краской темного цвета. Коэффициент полезного действия двигателя h = 0,86, причем 30 % потерь составляет тепловое излучение наружной поверхности двигателя, которая в процессе эксплуатации нагревается до 70 °С. Диаметр корпуса двигателя и размеры полости в стойке станка показаны на рис. П5.8, поверхности, обменивающиеся теплотой, имеют размер, перпендикулярный к плоскости чертежа, равный 480 мм.
Рассчитать температуру, до которой нагреваются внутренние поверхности полости в стойке станка в связи с тепловым излучением двигателя.
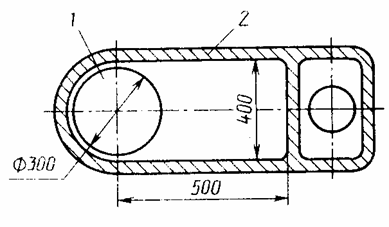
Рис. П5.8. Расположение электродвигателя в стойке станка
Алгоритм решения и комментарии к нему:
а) определить мощность теплового потока, излучаемого электродвигателем [W = 3000 (1 — 0,86) 0,3 = 126 Вт];
б) рассчитать площади поверхностей двигателя и стойки, участвующих в процессе лучистого теплообмена (S1» 0,45 м2; S2 » 0,97 м2);
в) определить коэффициенты облученности (j12=1; j21=0,45/0,97= 0,462);
г) рассчитать приведенную степень черноты, приняв по прил. 5 значения e1 = e2 = 0,9 (e2 » 0,86);
д) рассчитать значение М, имея в виду, что Q12/t=W =126Вт (М= 57,1);
е) при QS1=70°С рассчитать значение QS2 (QS2»27°С).
Ответ: Температура QS2»27°С.
Приложение 6
1.1 Чем отличаются друг от друга трех-, двух- и одномерные температурные поля?
1.2 Чем отличается квазистационарное температурное поле от стационарного и нестационарного?
1.3 Как расположены по отношению друг к другу векторы градиента температуры и плотности теплового потока?
1.4 Объясните физический смысл коэффициентов теплопроводности и температуропроводности материала.
1.5 Сформулируйте закон Фурье.
1.6 В чем различие процессов теплообмена при естественной и вынужденной конвекции среды? Какие из критерия подобия можно не учитывать, если рассматривают теплообмен между твердым телом и спокойным воздухом?
1.7 В каком случае коэффициент теплоотдачи от поверхности нагретой плиты в спокойный воздух больше: если она поставлено на короткое ребро или на длинное?
1.8 Какие виды теплообмена происходят одновременно при конденсации жидкости на поверхности твердого тела?
1.9 Что такое тепловая цепь?
1.10 Напишите дифференциальное уравнение теплопроводности.
1.11 Сформулируйте законы Кирхгофа и Стефана-Больцмана, относящиеся к процессам излучения.
1.12 Что такое приведенная степень черноты системы тел, от чего она зависит?
2.1 Для чего выполняется схематизация компонентов технологических подсистем при описании процессов теплообмена? Какими общими соображениями следует руководствоваться, принимая большую или меньшую степень детализации подсистемы при схематизации?
2.2 Каковы особенности быстродвижущихся источников теплоты?
2.3 Назовите различные виды граничных условий и дайте каждому из них краткую характеристику.
2.4 Из каких групп символов состоит код, описывающий особенности тепловых задач?
2.5 Перечислите и коротко охарактеризуйте аналитические методы решения дифференциального уравнения теплопроводности.
2.6 В чем состоит принцип конструирования решений в методе источников? Приведите примеры.
2.7 В чем преимущества и недостатки численных методов расчета по сравнению с аналитическими методами?
2.8 Кратко перечислите этапы решения дифференциального уравнения теплопроводности методами конечных разностей и конечных элементов.
3.1 В чем смысл обобщенного алгоритма теплофизического анализа?
3.2 Напишите уравнение инженерной методики расчета температур и расшифруйте значения сомножителей.
3.3 Какие виды теплообмена возникают в зоне резания?
3.4 Какие существуют пути управления тепловыми явлениями при резании?
3.5 Какие тепловые явления возникают в технологическом оборудовании?
ЛИТЕРАТУРА
1. Беляев Н. М., Рядно А. А. Методы теории теплопроводности: Учебн. пособие для вузов. Ч. 1. М.: Высшая школа, 1982. 327 с.
2. Бондарев В. А., Процкий А. Е., Гринкевич Р. Н. Теплотехника. Минск:Вышэйшая школа, 1976. 384 с.
3. Резников А. Н. Теплофизика процессов механической обработки материалов. М.: Машиностроение, 1981. 279 с.
4. Справочник по специальным функциям/Под ред. М. Абрамовица и И. Сти-ган: Пер. с англ. М.: Наука, 1979. 832 с.
5. Теплотехника: Учебник для вувов/А. П.Баскатов, Б. В. Берг, О. К. Витт и др.; Под общ. ред. А. П. Баскатова. М.: Энергоиздат, 1982. 264 с.