Рассмотрим пример решения задачи о назначениях. Четверо рабочих могут выполнять работы четырех видов. Стоимости (с_ij) выполнения i-м рабочим j-й работы приведены в ячейках диапазона A1:D4 (рис. 27).

В этой таблице строки соответствуют рабочим, а столбцы – работам. Необходимо составить план выполнения работ так, чтобы все работы были выполнены, каждый рабочий был загружен только на одной работе, а суммарная стоимость выполнения всех работ была минимальной. Отметим, что данная задача является сбалансированной, т. е. число работ совпадает с числом рабочих. Если задача не сбалансирована, то перед началом решения ее необходимо сбалансировать, введя недостающее число фиктивных строчек или столбцов с достаточно большими штрафными стоимостями работ.

Для решения данной задачи построим ее математическую модель. Пусть переменная x_ij = 1, если i-м рабочим выполняется j-я работа, и x_ij = 0, если i-м рабочим не выполняется j-я работа. Тогда модель имеет следующий вид:

Минимизировать

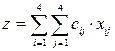
при ограничениях:

Для решения этой задачи с помощью средства поиска решений отведите под неизвестные диапазон ячеек F2:I5.

В ячейку J1 введите целевую функцию, вычисляющую стоимость работ:

=СУММПРОИЗВ(F2:I5;A1:D4).

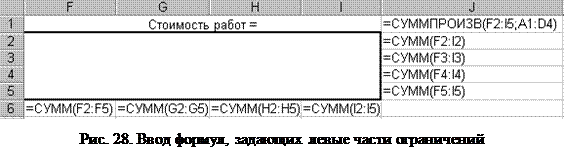
Введите формулы, задающие левые части ограничений (рис. 28).

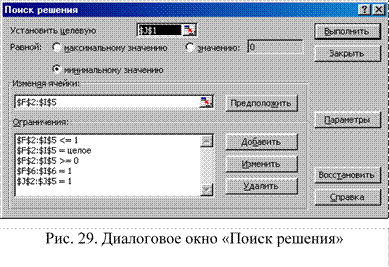
Выберите команду «Данные→Поиск решения» и заполните открывшееся диалоговое окно «Поиск решения», как показано на рис. 29.

Не забудьте в диалоговом окне «Параметры поиска решения» установить флажок «Линейная модель». После нажатия кнопки «Выполнить» средство поиска решений найдет оптимальное решение (рис. 30).

Таким образом, суммарная стоимость выполнения четырёх работ четырьмя рабочими будет минимальной, если 1-й рабочий будет выполнять 1-й вид работ, 2-й рабочий – 3-й вид работ, 3-й рабочий – 2-й вид работ, 4-й рабочий – 4-й вид работ.

Попробуйте изменить значения в ячейках F2:I5, убедитесь, что стоимость работ возрастет.