По курсу «Статистика» студенты, обучающиеся по специальности «Финансы и кредит», выполняют две контрольные работы: по разделу 1 (первая) и по разделу 2 (вторая), в соответствии с выбранным вариантом. Студенты других специальностей выполняют только первую контрольную работу.

1. Методические указания к выполнению контрольной работы № 1

Контрольная работа № 1 посвящена разделу 1 – общей теории статистики. Каждая контрольная работа состоит из двух частей: ответов на два теоретических вопроса и решения двух-трех задач.

Номер варианта выбирается в соответствии с начальной буквой фамилии студента по предлагаемой ниже таблице.

Начальная буква фамилии	Номер варианта	Начальная буква         фамилии	Номер варианта
А, Б	1	П, Р	8
В, Г	2	С, Т	9
Д, Е	3	У,Ф	10
Ж, З	4	Х, Ц	11
И, К	5	Ч, Ш	12
Л, М	6	Щ, Э	13
Н, О	7	Ю, Я	14

Ответы на поставленные вопросы должны быть исчерпывающими и конкретными, формулы должны быть с пояснениями, текст подкрепляется практическими примерами, делаются ссылки на используемые источники. Переписывание теоретического материала из учебной литературы – не допустимо.

В формулах при решении задачи необходимо давать пояснение каждой единицы измерения, после чего подставлять в них конкретные числовые значения.

Объем работы — не менее 12 листов ученической тетради. При оформлении работы необходимо оставлять поля для замечаний рецензента. В конце работы приводится список использованных источников в соответствии с требованиями ГОСТа, ставится подпись и дата выполнения работы.

Краткий теоретический материала, знание которого необходимо для решения задач 1 и 2.

1.1. Статистическое наблюдение, сводка и группировка.

Статистическое наблюдение – это первая стадия экономико-статистического исследования и представляющая собой сбор данных об изучаемых процессах и явлениях.

Объектом наблюдения называется явление или их совокупность, информацию о которых собирают в процессе статистического наблюдения.

В результате первой стадии статистического исследования получают статистическую информацию, представляющую собой большое количество разрозненных первичных сведений об отдельных единицах объекта исследования. На следующей стадии (этапе сводки) полученная информация систематизируется, выделяются закономерности и данные обобщаются в группы. Статистическая сводка – это научно организованная работа по обработке материалов статистического наблюдения, которая включает в себя систематизацию, группировку данных, составление таблиц, подсчет групповых и общих итогов, т.е. приведение информацию к виду, удобному для анализа. Статистическая сводка бывает простой — содержащей лишь подсчет общих итогов и сложной – в виде группировки данных в группы по однородному признаку, подведению итогов по ним и сведение полученных результатов в таблицу.

Статистическая группировка представляет собой процесс образования однородных групп на основе расчленения статистической совокупности на части или объединения изучаемых единиц в частные совокупности по существенным для них признакам. Статистическая группировка в зависимости от решаемых задач бывает 3-х видов: типологическая; структурная; аналитическая (факторная).

К особому виду группировок относят классификацию.

Ряд распределения является простейшей группировкой и представляет собой упорядоченное распределение единиц изучаемой совокупности по значению варьирующего признака. Вариант ряда распределения – это отдельные числовые значения количественного признака. Частота – численности отдельных вариантов, их сумма называется объемом совокупности. Ряд распределения, построенный на основе качественного признака называется атрибутивным, а на основе количественного – вариационным. Также различают дискретный вариационный ряд распределения, выражаемый одним целым числом; и интервальный вариационный ряд, в котором признак принимает различные значения в пределах интервала.

При построении вариационного ряда распределения определяют оптимальное количество групп (n) и величину интервала, в пределах которой изменяется вариационный признак (h). Оптимальное количество групп находится по формуле Стерджесса:

n=1+3,322*lgN,

где N – количество единиц совокупности.

Также можно воспользоваться следующей таблицей.

	15-24	25-44	45-89	90-179	180-359	360-719
n	5	6	7	8	9	10

Величина равного интервала определяется по формуле:

,

где  и - максимальное и минимальное значение признака.

Задача 1.

В таблице приведены данные по 25 предприятиям одной из отраслей ДВ:

№ предприятия	Выпуск продукции, млн. р.	Численность работающих, чел.	№ предприятия	Выпуск продукции, млн. р.	Численность работающих, чел.
1	52,5	230	13	58,9	270
2	62,3	350	14	62,3	360
3	45,4	150	15	68,9	390
4	72,1	420	16	54,1	250
5	85,6	520	17	58,2	265
6	87,1	570	18	47,5	185
7	98,2	690	19	49,8	200
8	50,0	200	20	72,1	425
9	56,3	245	21	80,2	510
10	102,2	800	22	86,9	555
11	87,3	505	23	93,5	650
12	47,4	170	24	58,1	260
			25	97,1	685

1. Произведите группировку предприятий по размеру выпуска продукции.

2. Подсчитайте по каждой группе объем выпуска продукции и численность работающих.

3. Укажите, какая из групп является наиболее типичной для предприятий отрасли.

4. Постройте график зависимости между размером выпуска продукции и численностью работающих.

Задача 2.

По данным таблицы 1 произведите группировку предприятий по численности работающих, укажите, к какому виду группировок принадлежит данная группировка, подсчитайте по каждой группе объем выпуска продукции и численность работающих, на графике покажите зависимость между численностью работающих и объемом выпуска продукции.

Краткий теоретический материала, знание которого необходимо для решения задач 3-5.

1.2. Абсолютные и относительные показатели.

Абсолютные и относительные показатели по своей сущности являются обобщающими показателями, характеризующими общественные явления и процессы с количественной стороны.

Абсолютные величины – это именованные числа, имеющие определенную размерность и единицы измерения, т. е. характеризуют размер (уровень, объем) общественных явлений в конкретных условиях места и времени. В зависимости от причин и целей анализа применяют натуральные (тонны, литры, метры, штуки), условно-натуральные (условное топливо при пересчете различных видов топлива), денежные (стоимостные) —  (рубль, доллар, евро) и трудовые (человеко-день, человеко-час) единицы измерения.

Относительные величины – это обобщающий показатель, представляющий собой частное от деления одного абсолютного показателя на другой. Числитель – сравниваемая величина, знаменатель называют базой сравнения. Как правило база сравнения принимает следующие значения: 1, 100, 1000, 10000. Если основание (база сравнения) равно 1, то относительная величина показывает какую долю текущая величина составляет от базисной, или во сколько раз она больше. Если база сравнения равна 100, то относительная величина выражается в процентах (%), если база сравнения равна 1000 – в промилле (%о), 10000 – в децимилле (%оо).

По своему содержанию и в зависимости от задач различают следующие виды относительных величин:

1. Относительные величины выполнения планового задания – отношение уровня планируемого на предстоящий период (), к уровню, достигнутого в предыдущем периоде ():                             ВПЗ =

2. Относительные величины выполнения плана – отношение фактически достигнутого уровня в текущем периоде () к уровню планируемого показателя за этот же период ():                                      ОВП =

3. Относительные показатели динамики характеризуют изменение уровня развития какого-либо явления во времени и определяются путем деления уровня признака за определенный период или момент времени () на уровень этого же признака в предыдущем периоде (). При переменной базе сравнения () получают цепные показатели динамики, при постоянной базе сравнения () – базисные. Относительные показатели динамики иначе называются темпами роста и выражаются в коэффициентах или процентах:

,

4. Относительные показатели структуры характеризуют состав, долю, удельный вес элементов во всем объеме совокупности и представляет собой отношение части единиц совокупности () ко всему объему совокупности ():

5. Относительные показатели интенсивности показывают степень развития явления или степень насыщенности явления в определенной среде и могут выражаться в кратных отношениях, процентах, промилле, и др.

6. Относительные показатели координации характеризуют отношения частей изучаемой совокупности к одной из них, которая принимается за базу сравнения.

7. Относительные показатели сравнения характеризуют отношения одноименных абсолютных показателей к одинаковому моменту или периоду времени, но к различным объектам или территориям.

Задача 3

Инвестиции в основной капитал (млн. руб.) в экономику Дальнего Востока характеризовались следующими данными:

     1994 г.      1995 г.      1996 г.      1997 г.    1998 г.     1999 г. 

     6466         13961        19127       20553      20794       40624 

Рассчитайте цепные и базисные относительные показатели динамики.

Задача 4

Численность профессорско-преподавательского персонала (на начало учебного года; тыс. чел.) в государственных высших учебных заведениях характеризовались следующими данными:

Годы	2002/2003	2003/2004
Численность профессорско-преподавательского состава – всего	249,6	255,9
Доктор наук	24,3	25,8
Кандидат наук	120,2	122,4
Профессор	24,6	25,7
Доцент	87,1	89,3
Другие категории ППС: без ученой степени Без ученого звания	105,1 137,9	107,7 140,9

Рассчитайте относительные величины структуры профессорско-преподавательского состава за 2002/2003 и 2003/2004 учебные годы. Дайте сравнительный анализ изменения структуры.

Задача 5

Деятельность строительно-монтажных управлений (СМУ) треста характеризовались следующими данными:

№ СМУ	План – 2004 г. (млн. р.)	Фактически выполнено
1	180	189
2	250	280
3	220	210
Итого

Для проведения анализа деятельности СМУ рассчитайте относительные показатели выполнения плана по каждому СМУ и тресту в целом.

Краткий теоретический материал, знание которого необходимо для решения задач 6-9.

1.3.  Средние величины и показатели вариации.

Средняя величина является обобщающей характеристикой совокупности по качественно однородному признаку и показывает типичный уровень изучаемой совокупности.

Статистика применяет различные виды средних величин: арифметическая, гармоническая, квадратическая, геометрическая (могут быть как простые, так и взвешенные, учитывающие частоту ряда распределения), а также структурные средние -мода и медиана. В статистике наибольшее распространение получила средняя арифметическая.

Средняя арифметическая простая равна сумме значений признака, деленной на их число и рассчитывается по формуле:

,

где х – значение осредняемого признака (варианта); n – число единиц признака.

Средняя арифметическая взвешенная применяется когда данные представлены в виде рядов распределения, в которых значения признака (х) объединены в группы с разными частотами () и рассчитывается по формуле:

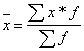
Наиболее часто встречающееся в изучаемой совокупности значение признака называется модой. В дискретном ряде распределения мода – это вариант с наибольшей частотой. Медиана – это вариант, расположенный в середине вариационного ряда и делящий его на две равные части.

Основные обобщающие показатели вариации – дисперсия, среднее квадратическое отклонение, коэффициент вариации, которые применяются для измерения степени колеблемости значений признака от средней.

Дисперсия () – это средняя арифметическая квадратов отклонений отдельных значений признака от их средней величины. Дисперсия может вычисляться по формуле средней арифметической простой или взвешенной, в зависимости от исходных данных.

Дисперсия простая:                     ;

Дисперсия взвешенная:             .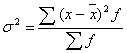

Среднее квадратическое отклонение ()  представляет собой корень квадратный из дисперсии и рассчитывается по формулам:

Среднее квадратическое отклонение невзвешенное:

;

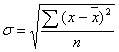Среднее квадратическое отклонение взвешенное:

.

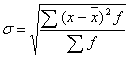Среднее квадратическое  отклонение является абсолютной мерой вариации признака в совокупности и выражается в единицах измерения варьирующегося признака (метрах, кг, тоннах, рублях и т.п.).

Коэффициент вариации () – это относительный показатель вариации, величина которого показывает степень вариации признаков, насколько однороден состав совокупности. Чем меньше коэффициент вариации, тем более однородна совокупность по составу, тем меньше разброс значений признака вокруг средней величины. Коэффициент вариации находится по формуле:

.