В каждом задании выбраны в качестве примеров различные предметные области. Возможно их использование в отдельных случаях как базовых. В самостоятельной работе необходимо кратко описать теоретические основы вопроса.

Задание 1. В качестве предметной области выберем фирму, занимающуюся оптовой торговлей парфюмерии, косметики и строительных материалов.

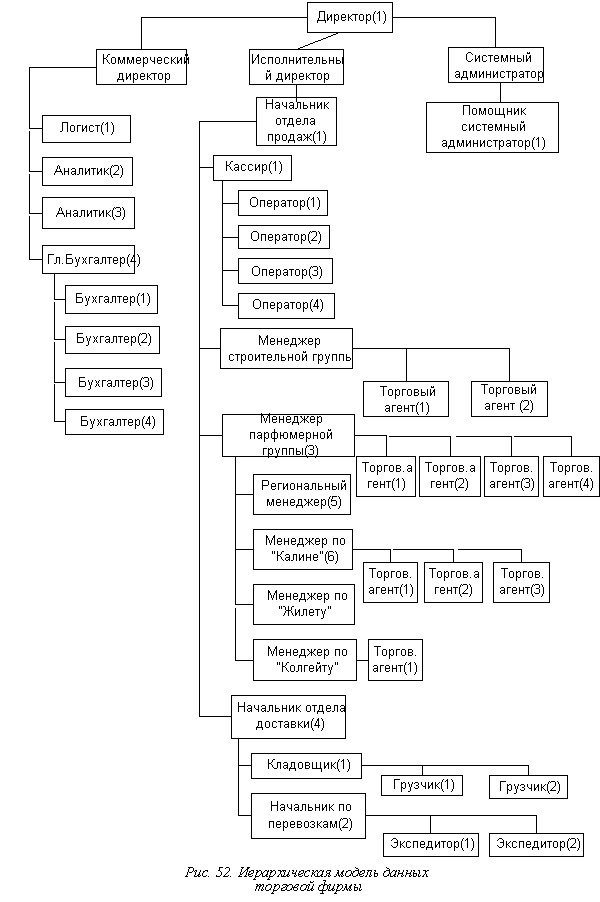
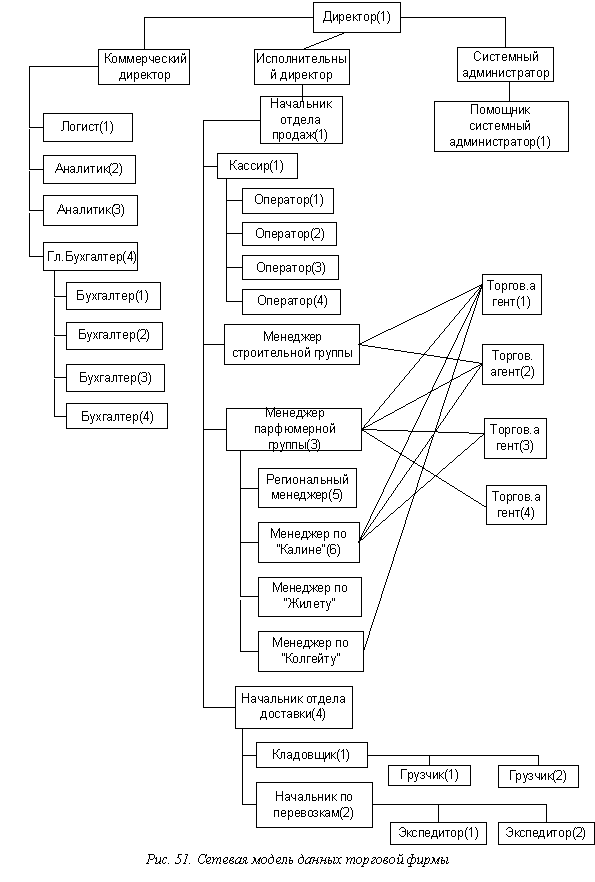Построим модели данных (рис. 50, 51, 52).

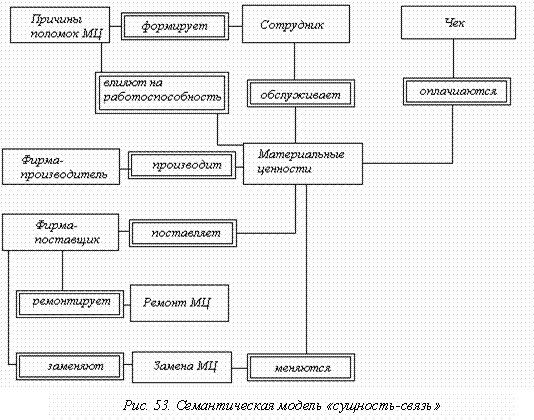Задание 2. Семантическая модель «сущность-связь» информационной системы  управления материальными ресурсами образовательного учреждения (рис. 53).

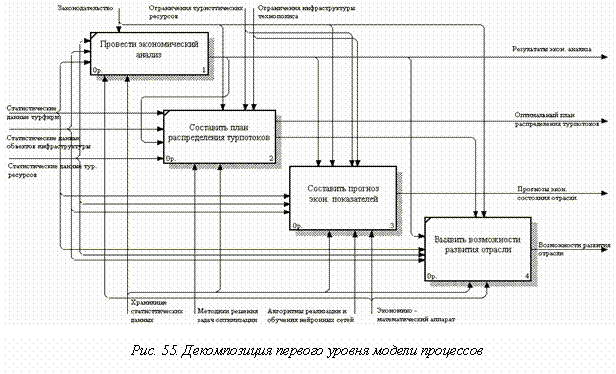
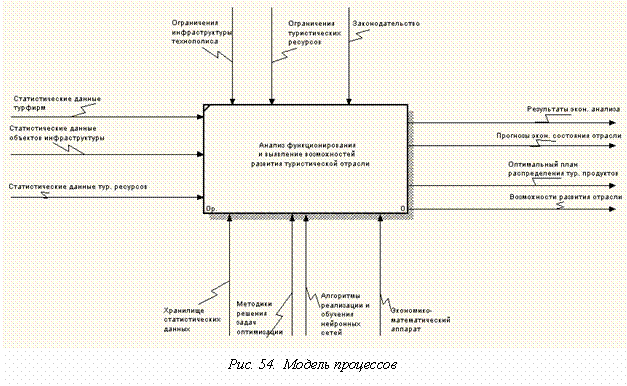Задание 3. SADT-модель процессов данных информационной системы “Анализ функционирования и выявление возможностей развития туристической отрасли»    (рис. 54, 55).

Задание 4. Описать автомат, построить таблицу и диаграмму состояний и проанализировать ее.

Задача. Пусть дан некоторый автомат М, который исходя из начального состояния S₀ перерабатывает входную информацию в выход следующим образом:

а – если считал последовательно 010,

b — если считал последовательно 101,

с – если считал 000,

d – в остальных случаях.

Решение. Входной алфавит А={0, 1}, выходной алфавит Z={a, b, c, d}. Опишем внутренние состояния и функции перехода и функцию выхода.

S0 – начальное состояние, S1 – считал 0, S2 – считал 1, S3 – считал 00, S4 – считал 01, S5 – считал 10.

n:    (S0, 0) a s1, (S0, 1) a s2, (S1, 0) a s3, (S1, 1) a s4, (S2, 0) a s5, (S2, 1) a s2, (S3 , 0) a s3, (S3 , 1) a s4, (S4 , 0) a s5, (S4 , 1) a s2, (S5 , 0) a s3, (S5 , 1) a s4.

x:    (S0, 0) a d, (S0, 1) a d, (S1, 0) a d, (S1, 1) a d, (S2, 0) a d, (S2, 1) a d, (S3 , 0) a c, (S3 , 1) a d, (S4 , 0) a a, (S4 , 1) a d, (S5 , 0) a d, (S5 , 1) a b.

Построим таблицу и диаграмму состояний (табл. 12, рис. 56).

Таблица 12

Текущее состояние	Функция перехода в новое состояние		Функция выхода
	0	1	0	1
S0	S1	S2	d	d
S1	S3	S4	d	d
S2	S5	S2	d	d
S3	S3	S4	c	d
S4	S5	S2	a	d
S5	S3	S4	d	b

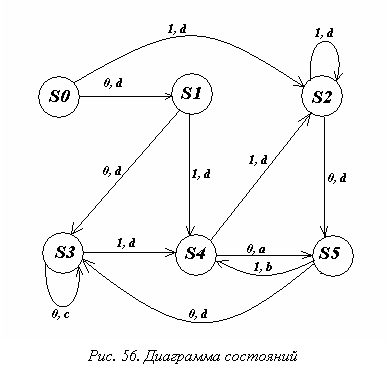
Анализ диаграммы автомата: состояние s₀ недоступно из других состояний, причем, начиная работу с него, автомат обязательно переходит в другое состояние; в состояние s₁ можно попасть только из состояния s₀; все состояния, кроме s₀, являются достижимыми из других состояний.

Задание 5.

В рассматриваемом периоде на ВЦ СУ решаются следую­щие задачи:

тип 1 — перспективное планирование;

тип 2 — недельное планирование;

тип 3 — корректировка технологических процессов в ре­жиме реального времени.

Принята система диспетчеризации, при которой задачи типа 3 имеют приоритет перед задачами типа 2 и 1, а задачи типа 2 имеют приоритет перед задачами типа 1.

На основе обработки статистических данных установлено, что характеристики имеют значения, представленные в табл. 13.

Если прервано обслуживание заявки, то после ожидания решение данной задачи продолжается.

Вычислим эффективность дисциплины по штрафам по сравнению с дисциплиной «первым пришел — первым обслу­жен».

Решение.

1.Найдем среднее время пребывания заявок в системе при приоритетном обслуживании по формуле (2), ч:

Таблица 13

Результаты обработки статистических данных

Тип	Приоритетная система									Система без приоритетов
зада­чи	, р.		, 1/ч		,ч		,ч		, ч	р.	,1/ч	,ч	,ч	, ч
1	1,6	0,05		0,60		0,40		3,0		1,6	0,05	0,3	0,7	3,0
2	2,2	0,2		0,20		0,50		1,0		2,2	0,2	0,4	0,8	1,0
3	40,0	3		0,01		0,07		0,2		40,0	3	0,05	0,2	0,2

;

;

;

2. Определим среднее время пребывания заявок в системе при бесприоритетном обслуживании, ч:

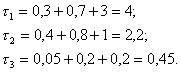
3. Найдем потери при приоритетном обслуживании по формуле (4):

 р.

4. Вычислим потери при бесприоритетном обслуживании по формуле (4):

 р.

5.Определим относительный критерий эффективности диспетчеризации обработки информации:

.

6. Рассчитаем приращение эффекта в результате примене­ния приоритетного обслуживания:

 р.

Задание 6.

Определим эффективность дисциплины по эквивалентному изменению производительности по сравнению с бесприоритет­ной дисциплиной при отсутствии прерывания в обслуживании, если же обслуживание начато, то оно ведется до конца, несмотря на приход приоритетной заявки (относительный приоритет).

Имеются две системы обслуживания: q — «первый пришел — первым обслужен» и s — в первую очередь обслуживаются за­дачи корректировки технологического процесса (тип 3), затем недельного планирования (тип 2) и, наконец, перспективного планирования (тип 1), куда относятся задачи планирования на срок более одной недели.

Возьмем статистические данные предыдущего задачи, но не будем учитывать прерывание. Оставим среднее время ожидания до начала обслуживания и время «чистого» обслуживания.

Таблица 14

Результаты обработки статистических данных

Тип		Приоритетная система									Система без приоритетов
зада­чи		, р.		, 1/ч		,ч		,ч		, ч	р.	,1/ч	,ч	,ч	, ч
1	1,6		0,05		0,6		0,4		3,0		1,6	0,05	0,3	0,7	3,0
2	2,2		0,2		0,2		0,5		1,0		2,2	0,2	0,4	0,8	1,0
3	40,0		0,3		0,01		0,07		0,2		40,0	0,3	0,05	0,2	0,2

Определим эффективность дисциплины по эквивалентному изменению производительности с учетом пребывания заявок в очереди до начала обслуживания.

Представим исходные статистические данные после обра­ботки в табл. 15.

Решение.

1. Определим общую загрузку системы:

2. Рассчитаем штраф в бесприоритетной системе по фор­муле (4):

 р.

Таблица 15

Результаты обработки статистических данных

Тип	Приоритетная система					Система без приоритетов
задачи	, р.	,1/ч		,ч	,ч	р.	,1/ч	,ч	,ч
1	1,6		0,05	0,6	3	1,6	0,05	0,3	3
2	2,2		0,2	0,2	1	2,2	0,2	0,4	1
3	40,0		3	0,01	0,2	40,0	3	0,5	0,2

3. Штраф в системе с установленными приоритетами по формуле (4) составил:

 р.

4. Определим эффективность дисциплины диспетчеризации по сравнению с бесприоритетной системой по формуле (6):

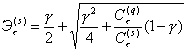
Следовательно, введение приоритетов обслуживания задач на ВЦ выигрышно по про­изводительности.