Задача № 1. Разработать программу, которая выводит на экран замкнутый многоугольник и заполняет его буквами «О» размером 8×8 пикселов.
Решение. Для того, чтобы закрасить многоугольник произвольным шаблоном размером 8х8 пикселов, необходимо воспользоваться функцией
void setfillpattern(char far *pattern, int color).
Шаблон устанавливается с помощью массива pattern. В случае буквы «О» массив pattern задаётся следующим образом:
char pattern[]=
{
0x1C, // 00011100
0x22, // 00
0x41, // 01
0x41, // 01
0x41, // 01
0x22, // 00
0x1C, // 00011100
0x0 // 00000000
};
Программа
#include <graphics.h>
#include <conio.h>
#include <stdlib.h>
// Шаблон буквы О
char pattern[]=
{
0x1C, // 00011100
0x22, // 00
0x41, // 01
0x41, // 01
0x41, // 01
0x22, // 00
0x1C, // 00011100
0x0 // 00000000
};
// Координаты вершин многоугольника
int poly[]=
{
30, 10,
50, 0,
200, 100,
100, 150,
50, 30,
};
void main()
{
// Инициализация графики
int gdriver=DETECT, gmode;
initgraph(&gdriver, &gmode, "");
// Установка палитры закраски
setfillpattern(pattern, WHITE);
// Вывод закрашенного многоугольника
fillpoly(sizeof(poly)/(sizeof(int)*2), poly);
getch(); // Ожидание нажатия клавиши
closegraph(); // Выход из графического режима
}
Результат работы программы
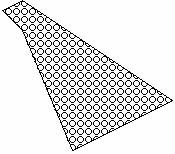
Задача № 2. Пусть задан отрезок с экранными координатами ((1, 1), (6, 3)). Рассмотреть на примере вывода этого отрезка алгоритм Брезенхема и записать последовательность точек, которые будут сгенерированы этим алгоритмом.
Решение. Для решения этой задачи можно применить как целочисленную версию алгоритма Брезенхема, так и версию, использующую вычисления с вещественными числами. Рассмотрим версию алгоритма Брезенхема, использующую вычисления с вещественными числами.
x0 = 1, x1 = 6, y0 = 1, y1 = 3, ∆x = x1 – x0 = 5, ∆y = y1 – y0 = 2, ∆y/∆x = 0.4.
Т.к. ∆x > 0, ∆y > 0 и ∆y < ∆x, то x увеличивается на 1.
- x = 1, y = 1, d = 0, генерируется точка (1, 1).
- x = x + 1 = 2, d = d + ∆y / ∆x = 0.4. Т.к. -0.5 ≤ d < 0.5, то y не изменяется. Генерируется точка (2, 1).
- x = x + 1 = 3, d = d + 0.4 = 0.8. Т.к. d > 0.5, то y = y + 1 = 2 и d = d – 1 = -0.2. Генерируется точка (3, 2).
- x = x + 1 = 4, d = d + 0.4 = 0.2. Т.к. -0.5 ≤ d < 0.5, то y не изменяется. Генерируется точка (4, 2).
- x = x + 1 = 5, d = d + 0.4 = 0.6. Т.к. d > 0.5, то y = y + 1 = 3 и d = d – 1 = -0.4. Генерируется точка (5, 3).
- x = x + 1 = 6, d = d + 0.4 = 0. Т.к. -0.5 ≤ d < 0.5, то y не изменяется. Генерируется точка (6, 3).
В результате будет сгенерирована следующая последовательность точек: (1, 1), (2, 1), (3, 2), (4, 2), (5, 3), (6, 3).
Задача № 3. Пусть известны координаты точки S(2, 4, 5) и плоскость P, которая задаётся векторами u1 = (0, 1, 0), u2 = (0, 0, 1) и r0 = (1, 1, 1). Найти координаты (x′, y′) параллельной проекции точки S на плоскость P в направлении вектора u = (1, 0.4, 0.5).
Решение
Воспользуемся следующими формулами:
x‘ = (r-r0,u2,u) / (u1,u2,u),
y‘ = -(r -r0,u1, u) / (u1,u2,u).
В нашем случае смешанное произведение (u1, u2, u) равно 1, т.к. 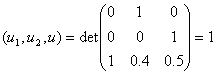 , и r–r0 = (1, 3, 4).
, и r–r0 = (1, 3, 4).
Поэтому
 ,
, 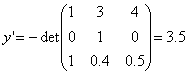 .
.
Ответ: x′ = 2.6, y′ = 3.5.
Задача № 4. Пусть известны координаты точки S(2, 5, 3) и плоскость P, которая задаётся векторами u1 = (0, 1, 0), u2 = (0, 0, 1) и r0 = (0.3, 0.7, 0.2). Найти координаты (x′, y′) центральной проекции точки S на плоскость P из точки наблюдения rv = (1, 1, 1).
Решение. Координаты x’, y’ вычисляются по формулам
x’ = (rV-r0,u2,r-rV) / (u1,u2,r-rV),
y’ = — (rV -r0,u1,r-rV) / (u1,u2,r-rV).
rv-r0 = (0.7, 0.3, 0.8); r = (2, 5, 3); r-rv = (1, 4, 2);
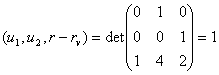 ;
; 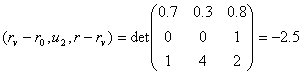 .
.
x′ = -2.5;
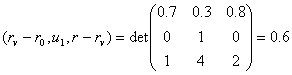 .
.
y′ = — 0.6;
Ответ: x′ = -2.5, y′ = — 0.6.
Задача № 5. Пусть заданы координаты точки S(2, 1, 3), вектор единичной длины ![]() и угол φ=600. Найти координаты точки S′, полученной поворотом точки S вокруг вектора u на угол φ.
и угол φ=600. Найти координаты точки S′, полученной поворотом точки S вокруг вектора u на угол φ.
Решение. Воспользуемся формулой r‘ = Ar, где
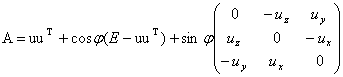 ,
, 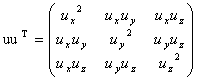 .
.
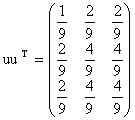 ,
, 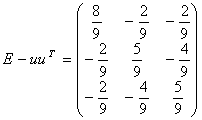 ,
,
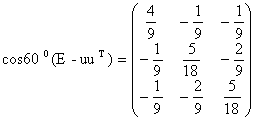 ,
,
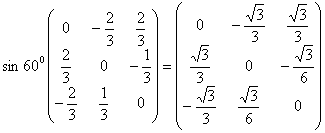 .
.
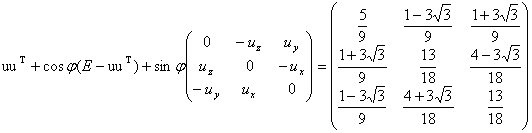 .
.
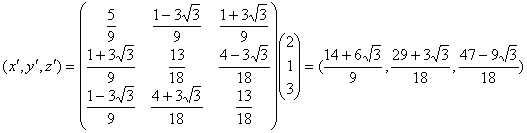 .
.
Ответ: ![]() .
.