Пусть A и B – нечеткие подмножества универсального множества E. Введем понятие расстояния r(A, B) между нечеткими множествами. При введении расстояния обычно предъявляются следующие требования:

·  r(A, B) ³ 0 – неотрицательность;

·  r(A, B) = r(B, A) – симметричность;

·  r(A, B) < r(A, C) + r(C, B).

К этим трем требованиям можно добавить четвертое: r(A, A) = 0.

Определим следующие расстояния по формулам:

Расстояние Хемминга (или линейное расстояние):

r(A, B) = .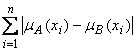

Очевидно, что r(A, B)Î[0, n].

Евклидово или квадратичное расстояние:

e(A, B) = 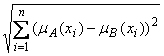, e(A, B) Î[0, ].

Относительное расстояние Хемминга:

r(A, B) = 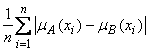, r(A, B) Î[0,1].

Относительное евклидово расстояние:

e(A, B) = 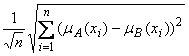, e(A, B) Î[0,1].

Расстояние Хемминга и квадратичное расстояние, в случае, когда E бесконечно, определяются аналогично с условием сходимости соответствующих сумм:

если E счетное, то

r(A, B) =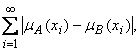 e(A, B) =;

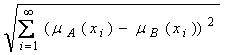если E = R (числовая ось), то

r(A, B) = 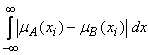, e(A, B) =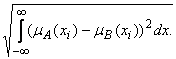

Замечание. Здесь приведены два наиболее часто встречающихся определения понятия расстояния. Разумеется, для нечетких множеств можно ввести и другие определения понятия расстояния.