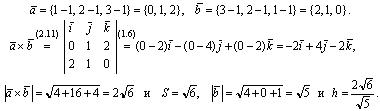1°.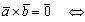
 — коллинеарные векторы;2°.
— коллинеарные векторы;2°.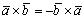 ;3°.
;3°.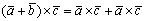 ;4°.
;4°.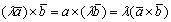 . ДоказательствоСвойство 1° Если хотя бы один из векторов нулевой, то свойство очевидно. Пусть
. ДоказательствоСвойство 1° Если хотя бы один из векторов нулевой, то свойство очевидно. Пусть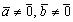 , тогда:если
, тогда:если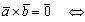 ,
,
то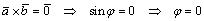 , либо
, либо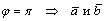 — коллинеарны;
— коллинеарны;
если  коллинеарны,
коллинеарны,
то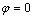 , либо
, либо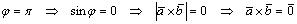 .
.
Свойство 2о Пусть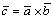 . Из определения векторного произведения векторов следует:
. Из определения векторного произведения векторов следует:
1)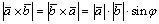 ;
;
2)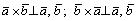 ;3)
;3) 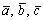 - правая тройка
- правая тройка 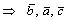 — левая тройка
— левая тройка 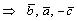 — правая тройка. Отсюда получаем:
— правая тройка. Отсюда получаем:
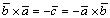
.
Свойства 3 о , 4 ° доказать самостоятельно. Найдем векторные произведения ортов осей координат:
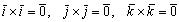 (свойство 1°);
(свойство 1°);  (правые тройки векторов);
(правые тройки векторов);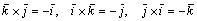 (левые тройки векторов).
(левые тройки векторов).
Используя полученные равенства, выразим векторное произведение через координаты сомножителей. Пусть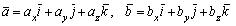 , тогда, используя свойства 1о — 4°, получаем:
, тогда, используя свойства 1о — 4°, получаем:
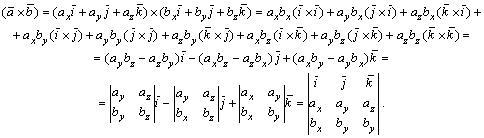
Таким образом,
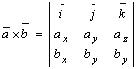
. (2.11)
Основные приложения векторного произведения
1)Вычисление площади треугольника (параллелограмма). Из курса математики средней школы известно, что площадь треугольника равна половине произведения его сторон на синус угла между ними , что совпадает с половиной модуля векторного произведения векторов, которые построены на сторонах треугольника. Таким образом,
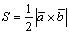
,
где S площадь треугольника с вершинами в точках
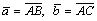
2) Вычисление высоты треугольника (параллелограмма).Вычислим площадь треугольника двумя способами:
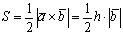
,
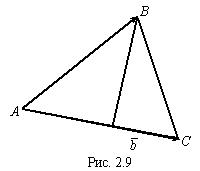
где h — высота треугольника, опущенная из вершины В (рис. 2.9). Из этого равенства получаем:
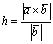
.
Пример. 2.1. Найти площадь треугольника с вершинами в точках А (1, 1, 1), В (1, 2, 3), С (3, 2, 1) и высоту, опущенную из вершины В на сторону АС (рис. 2.9). Решение. Пусть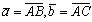 , тогда
, тогда