В n -мерном линейном пространстве любая упорядоченная линейно независимая система из n векторов является базисом. Доказательство очевидно (вытекает из определения базиса). В частности, любых три линейно независимых вектора в 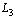образуют базис.Если 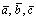— базис в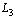, то равенство

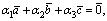
возможно лишь тогда, когда, т.е. система

,

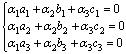
где 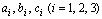— координаты векторов 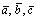в базисе соответственно, должна иметь единственное решение. Тогда по теореме 1.1 получаем условие линейной независимости трех векторов:

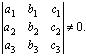
Если векторы 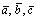образуют базис в L, то по определению базиса любой вектор 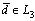можно представить в виде:

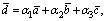
или, в координатной записи:

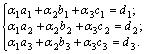
Числа 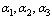называются координатами вектора 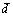в базисе.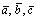