1 – 10. Найти пределы функций, не пользуясь правилом Лопиталя.
1. а)![]() ; б)
; б) 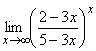 ;
;
в)  ; г)
; г) ![]() ;
;
2. а) ![]() ; б)
; б)  ;
;
в) ![]() ; г)
; г) ![]() ;
;
3. а) ![]() ; б)
; б) 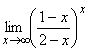 ;
;
в) ![]() ; г)
; г) ![]() ;
;
4. а) ![]() ; б)
; б) 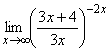 ;
;
в) ![]() ; г)
; г) 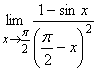 ;
;
5. а) ![]() ; б)
; б)  ;
;
в) ![]() ; г)
; г) ![]() ;
;
6. а) ![]() ; б)
; б) 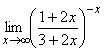 ;
;
в) ![]() ; г)
; г) ![]() ;
;
7. а) ![]() ; б)
; б) 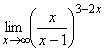 ;
;
в) ![]() ; г)
; г) 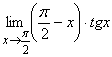 ;
;
8. а) ![]() ; б)
; б) 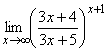 ;
;
в)  ; г)
; г) ![]() ;
;
1. а) ![]() ; б)
; б) 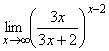 ;
;
в) ![]() ; г)
; г) ![]() ;
;
2. а) ![]() ; б)
; б) 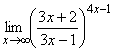 ;
;
в) ![]() ; г)
; г) 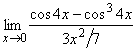 ;
;
11 – 20. Найти производные ![]() данных функций.
данных функций.
11. а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() ;
;
д) ![]() .
.
12. а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() ;
;
д) ![]() .
.
13. а)  ; б)
; б) 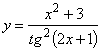 ;
;
в) ![]() ; г)
; г) ![]() ;
;
д) ![]() .
.
14. а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() ;
;
д) ![]() .
.
15. а) ![]() ; б)
; б) ![]() ;
;
в)  ; г)
; г) ![]() ;
;
д) ![]() .
.
16. а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() ;
;
д) ![]() .
.
17. а) 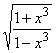 ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() ;
;
д) ![]() .
.
18. а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() ;
;
д) ![]() .
.
19. а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() ;
;
д) ![]() .
.
20. а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() ;
;
д) ![]() .
.
21 – 30. Найти ![]() и
и ![]() для функций:
для функций:
21. а) ![]() ; б)
; б)  .
.
22. а) ![]() ; б)
; б) 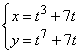 .
.
23. а) ![]() ; б)
; б) ![]() .
.
24. а) ![]() ; б)
; б)  .
.
25. а) ![]() ; б)
; б) 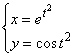 .
.
26. а) ![]() ; б)
; б) ![]() .
.
27. а) ![]() ; б)
; б) 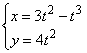 .
.
28. а) ![]() ; б)
; б) 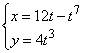 .
.
29. а) ![]() ; б)
; б) ![]() .
.
30. а) ![]() ; б)
; б) 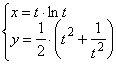 .
.
31 – 40. Найти а) ![]() ; б) значение
; б) значение ![]() при
при ![]() , используя понятие дифференциала функции.
, используя понятие дифференциала функции.
31. а) ![]() ; б)
; б) ![]() .
.
32. а) ![]() ; б)
; б) ![]() .
.
33. а) ![]() ; б)
; б) ![]() .
.
34. а) ![]() ; б)
; б) ![]() .
.
35. а) ![]() ; б)
; б) ![]() .
.
36. а) ![]() ; б)
; б) ![]() .
.
37. а) ![]() б)
б) ![]() .
.
38. а) ![]() ; б)
; б) ![]() .
.
39. а) ![]() ; б)
; б) ![]() .
.
40. а) ![]() ; б)
; б) ![]() .
.
41 – 50. Найти наибольшее и наименьшее значения функции ![]() на отрезке
на отрезке ![]() .
.
41. ![]() на
на ![]() .
.
42. ![]() на
на ![]() .
.
43. ![]() на
на ![]() .
.
44. ![]() на
на ![]() .
.
45. ![]() на
на ![]() .
.
46. ![]() на
на ![]() .
.
47. ![]() на
на ![]() .
.
48. ![]() на
на ![]() .
.
49. ![]() на
на ![]() .
.
50. ![]() на
на ![]() .
.
51. В равнобедренный треугольник с основанием 4 и углом при основании ![]() вписать параллелограмм наибольшей площади, так, чтобы одна из сторон лежала на основании, а другая на боковой стороне. Найти длины сторон параллелограмма.
вписать параллелограмм наибольшей площади, так, чтобы одна из сторон лежала на основании, а другая на боковой стороне. Найти длины сторон параллелограмма.
52. Требуется изготовить бак цилиндрической формы без верхней крышки объемом 50 л. Каковы должны быть его размеры, чтобы на его изготовление уходило как можно меньше жести?
53. Равнобедренный треугольник, вписанный в окружность радиусом 10, вращается вокруг прямой, проходящей через его вершину параллельно основанию. Найти высоту треугольника, если тело полученное в результате вращения, имеет наибольший объем.
54. Проволокой, длиной 4 м, надо огородить клумбу, имеющую форму кругового сектора. Какой должен быть радиус круга, чтобы площадь была наибольшей?
55. Периметр равнобедренного треугольника – 40. Найти основание этого треугольника, так, чтобы объем тела вращения этого треугольника вокруг основания был наибольший.
56. Найти наибольшую площадь прямоугольника, вписанного в полукруг радиуса ![]() .
.
57. Найти стороны прямоугольника наибольшей площади, вписанного в эллипс, с полуосями 10 и 20.
58. Найти радиус основания и высоту цилиндра наибольшего объема, вписанного в шар радиусом 30.
59. Найти радиус основания и высоту цилиндра с наибольшей боковой поверхностью, вписанного в конус высотой 20 и радиусом основания 10.
60. Окно имеет форму прямоугольника, завершающегося полукругом. Периметр окна равен 20 м. При каком радиусе полукруга, окно будет пропускать наибольшее количество света.
61 – 70. Вычислить пределы, используя правило Лопиталя.
61. а) ![]() , б)
, б) ![]() .
.
62. а) ![]() , б)
, б) ![]() .
.
63. а) ![]() , б)
, б) ![]() .
.
64. а) ![]() , б)
, б) ![]() .
.
65. а) ![]() , б)
, б) 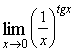 .
.
66. а) ![]() , б)
, б) ![]() .
.
67. а) ![]() , б)
, б) ![]() .
.
68. а) ![]() , б)
, б) ![]() .
.
69. а) ![]() , б)
, б) ![]() .
.
70. а) ![]() , б)
, б) 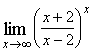 .
.
71 – 80. Исследовать методами дифференциального исчисления функцию ![]() и, используя результаты исследования, построить ее график.
и, используя результаты исследования, построить ее график.
71. а) 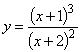 . б)
. б) ![]() .
.
72. а)  . б)
. б) ![]() .
.
73. а) ![]() . б)
. б) ![]() .
.
74. а)  . б)
. б) ![]() .
.
75. а) ![]() . б)
. б) ![]() .
.
76. а) ![]() . б)
. б) ![]() .
.
77. а) ![]() . б)
. б) ![]() .
.
78. а) ![]() . б)
. б) ![]() .
.
79. а)  . б)
. б) ![]() .
.
80. а) 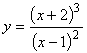 . б)
. б) ![]() .
.