Задано скалярное поле f(М) = f(х, y, z), которое определено и дифференцируемо в некоторой области V.

Определение. Градиентом функции в точке M(x, y, z) называется вектор, выходящий из точки М, имеющей своими координатами частные производные функции

Сравним с формулой нахождения производной функции по направлению:

то есть  является проекцией градиента на направление вектора  (другими словами, если известен угол  j  между векторами  grad f(M) и , то по определению проекции вектора на ось ).

Наибольшее значение cosj = 1, поэтому, если направление  совпадает с направлением градиента (j = 0), то

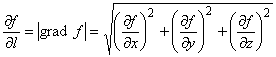
имеет в этом случае наибольшее значение.

Вектор gradf в данной точке М скалярного поля f(M) направлен в сторону наибыстрейшего роста функции в этой точке.

Уравнение f(х, у, z) = С определяет в скалярном поле некоторую поверхность уровня (см. раздел 1.1). Выбираем на ней точку М₀(х₀, у₀, z₀) и находим вектор

Но, как было рассмотрено выше, такие же координаты имеет нормаль к поверхности уровня, проходящей через точку М₀.

Пример 1.24. В скалярном поле u = f(x, y, z) = ху² + z² найти градиент в точке М₀(2, 1, –1) и вычислить производную поля в этой точке в направлении градиента.

Решение.

.

Следовательно, gradf(M₀) = 1 + 4 – 2.

Если направление  совпадает с направлением градиента, то

.