Пусть функция f(x) определена в точке x₀ и некоторой ее окрестности. Если существует  и , то функция f(x) называется непрерывной в точке x₀, а x₀ называется точкой непрерывности функции f(x).

На языке логики равенство   описывается формулой:

"e>0 $d>0 "xÎ(x₀ – d, x₀ + d) |f(x) – f(x₀)| < e .

Используя понятия односторонних пределов, можно перефразировать определение так: функция называется непрерывной в точке x₀, если она определена в точке x₀ и некоторой ее окрестности, если существуютf(x), f(x) и

f(x) = f(x) = f(x₀).

Иногда приходится рассматривать непрерывность функции в точке x₀ справа или слева. Пусть функция определена в точке x₀ и некоторой ее левой полуокрестности.

Если f(x) = f(x₀), то говорят, что f(x) непрерывна в точке x₀ слева.

Аналогично определяется непрерывность справа.

Пример 1. Функция f(x) = x³ определена на R.

Покажем, что f(x) непрерывна в точке x₀ = 2.

Действительно, f(2) = 2³ = 8, f(x) = x³ = 8, f(x) = f(2), значит, f(x) = x³ непрерывна в точке x₀ = 2.

Пример 2.  f(x) = .

Покажем, что f(x) непрерывна в точке x₀ = 0:

f(0) = 0, f(x) = 2x = 0, f(x) = sinx = 0.

Так какf(x) = f(x) = f(0), то непрерывность функции f(x) в точке x₀ = 0 доказана.

Дадим определение точек разрыва.

Пусть f(x) определена в окрестности точки x₀, но может быть не определена в x₀.

Точка x₀ называется точкой разрыва для функции f(x), если в точке x₀ функция f(x) не определена, или f(x) не существует, илиf(x) ¹ f(x₀).

Пример 3. Функция f(x) =  не определена в точке x₀ = 0, но определена в любой окрестности этой точки, поэтому x₀ = 0 является точкой разрыва для f(x).

Пример 4. Функция f(x) =  не определена в точке x₀ = 3, x₀ = 3 – точка разрыва для f(x).

Пример 5. Пусть E(x) = «целая часть числа x», т.е. E(x) равно наибольшему целому числу, не превосходящему x₀. Так E = 1,   E(5) = 5,   E(p) = 3,   E(0) = 0,   E(–0,5) = –1 и т.д. График y = E(x) представлен на рис. 1.14.   Для   x₀ = 2:   E(2) = 2, E(x) = 1, E(x) = 2.

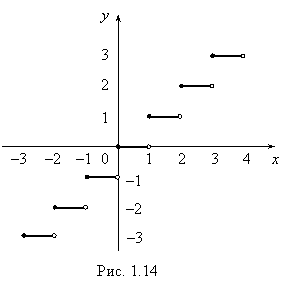Так как E(x) ¹ E(x), то E(x) в точке x₀ = 2 имеет разрыв, как и в любой другой целочисленной точке. Различают точки разрыва первого рода и второго рода.

Точка разрыва x₀ для функции f(x) называется точкой разрыва первого рода, если существуют (конечные) пределы:  f(x) и f(x). В противном случае x₀ – точка разрыва второго рода. В примере 5 точка x₀ = 2 является точкой разрыва первого рода, так как существуют пределы E(x) и E(x). В примере 4   x₀ = 3 – точка разрыва второго рода, так как  = –¥,  = +¥.

Точка x₀ разрыва первого рода, для которойf(x) = f(x), называется точкой устранимого разрыва. Такой является точка x₀ в примере 3. Если рассмотреть функцию j(x) =  , то j(x) непрерывна в точке x₀ = 0, так как j(x) = =  = 1 и j(0) = 1. Доопределив функцию в точке x₀ = 0, мы устранили разрыв.

Рассмотрим операции над непрерывными функциями.

Теорема 1. Если функции f₁(x) и f₂(x) непрерывны в точке x₀, то их сумма и произведение также непрерывны в точке x₀. Если, кроме того, f₂(x₀) ¹ 0, то частное также непрерывно в точке x₀.

Доказательство. Доказательство основано на свойствах пределов. Докажем, например, что сумма непрерывных функций непрерывна. Функции f₁(x),  f₂(x) непрерывны в точке x₀, поэтому f₁(x) = f₁(x₀), f₂(x) = f₂(x₀). Применяя теорему о пределе суммы двух функций, получим:

(f₁(x) + f₂(x)) = f₁(x) + f₂(x) = f₁(x₀) + f₂(x₀),

что означает непрерывность f₁(x) + f₂(x) в точке x₀. Аналогично для других утверждений теоремы. Заметим, что формулуf(x) = f(x₀) (определяющую непрерывность функции f(x) в точке x₀) можно записать в виде: f(x) = f(x), так как x = x₀. Эта формула означает, что при нахождении предела непрерывной функции можно переходить к пределу под знаком функции.

Теорема 2. Если функция u = j(x) непрерывна в точке x₀, а функция y = f(u) непрерывна в точке u₀ = j(x₀), то сложная функция y = f(j(x)) непрерывна в точке x₀.

Доказательство. Покажем, что f(j(x)) = f(j(x₀)). Действительно, из непрерывности функции j(x) имеем: j(x) = j(x₀) = u₀, т.е. при x ® x₀ следует, что u ® u₀. Далее, из непрерывности функции f(u) получаем:

f(j(x)) = f(u) = f(u₀) = f(j(x₀)).

Теорема доказана.

Установим непрерывность некоторых элементарных функций:

1. Всякая постоянная функция y = C непрерывна в каждой точке x₀ÎR, так как C = C.

2. Функция y = x непрерывна в любой точке x₀, так как x = x₀. Тогда функция y = Cxⁿ, где n Î N, непрерывна на всей числовой оси, как произведение непрерывных функций.

3. Любой многочлен: y = a₀ + a₁x + a₂x² + …+ a_nxⁿ, непрерывен в каждой точке числовой оси, как сумма непрерывных функций.

4. Всякая рациональная дробь, являющаяся отношением двух многочленов , непрерывна во всех точках, в которых многочлен Q(x) не обращается в 0.

5. Функция y = sinx,  y = cosx непрерывны в точке x₀ = 0, так как

sinx = 0, sin0 = 0,  cosx = 1, cos0 = 1, т.е. sinx = sin0 и cosx = cos0

(Это было доказано в разд. 1.9 ).

Сформулируем без доказательств следующую теорему.

Теорема 3. Всякая элементарная функция непрерывна в каждой точке, в которой она определена.

Если функция f(x) непрерывна в каждой точке интервала (a, b), то говорят, что f(x) непрерывна на интервале (a, b). 

Пример 6. Функция f(x) =  непрерывна на интервалах (–¥, 3) и (3, +¥), так как при x₀ ¹ 3:   f(x) =  = f(x₀).