В различных исследованиях используются формулы, полученные на основании эксперимента. Одним из таких способов получения формул является метод наименьших квадратов, который применяется для обработки результатов наблюдений. Пусть в результате опыта получена таблица значений функции у = f(x) для n значений независимой переменной х, т.е. имеем n точек (х1, у1), (х2, у2), …, (хn, уn), найденных экспериментально.
Нужно функцию задать аналитически, т.е. формулой. В общем случае рассматривают полином степени m: у = А0 + A1x + A2x2 +…+ Amхm.
Коэффициенты А0, A1, A2, …, Am определяют так, чтобы кривая как можно ближе проходила от всех n заданных точек, т.е. чтобы сумма квадратов разностей значений уi, получаемых экспериментально, и значений функций у(хi) была бы наименьшей.
Для определения степени m полинома заносят экспериментальные точки на координатную плоскость Оху. Если они примерно располагаются по одной прямой, то зависимость между х и у близка к линейной и
у = А0 + А1х.
Если опытные данные таковы, что при построении графика они располагаются вблизи некоторой параболы, то можно искать приближенную зависимость в виде
у = А0 + A1x + A2x2.
Рассмотрим более подробно этот случай. Коэффициенты А0, А1, А2 находим из условия, что сумма
![]()
имеет наименьшее значение.
Таким образом, перед нами поставлена задача нахождения наименьшего значения функции трех переменных А0, А1, А2. Воспользуемся необходимым условием экстремума функции трех переменных:
![]() .
.
Вычисляя производные, получаем

так как хi и уi заданы, то получаем для нахождения коэффициентов А0, А1, А2 линейную систему трех уравнений:
 (1.3)
(1.3)
Решение этой системы определяет линию (параболу), которая представляет найденную экспериментальную функцию.
Пример 1.25. Пусть в результате эксперимента получены значения функции при различных значениях аргумента:
|
х |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1,0 |
|
у |
2,130 |
2,153 |
2,161 |
2,151 |
2,128 |
2,080 |
2,026 |
1,859 |
1,875 |
1,772 |
Найти аналитическую зависимость переменной y от x наиболее правильно представляющую экспериментальные данные.
Решение. Изображаем точки на плоскости (рис. 1.5).
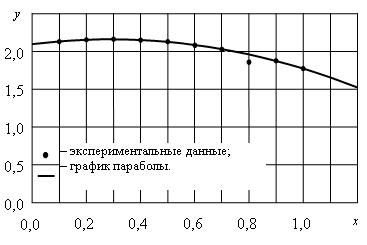
Рис. 1.5. Иллюстрация метода наименьших квадратов второго порядка
Ищем коэффициенты в уравнении параболы у = А0 + А1х + А2х2, здесь п = 10. Для решения системы (1.3) нужно вычислить суммы:

Все результаты занесем в таблицу.
Таблица 1.1 Промежуточные результаты в методе наименьших квадратов
|
п |
х |
х2 |
уi |
Суммы |
увыч= у(хi) |
d = увыч – уэксп |
|
1. |
0,1 |
0,01 |
2,1300 |
|
2,1318 |
+0,0019 |
|
2. |
0,2 |
0,04 |
2,1532 |
|
2,1531 |
-0,0001 |
|
3. |
0,3 |
0,09 |
2,1611 |
|
2,1590 |
-0,0021 |
|
4. |
0,4 |
0,16 |
2,1516 |
|
2,1497 |
-0,0019 |
|
5. |
0,5 |
0,25 |
2,1282 |
2,1250 |
-0,0032 |
|
|
6. |
0,6 |
0,36 |
2,0807 |
|
2,0851 |
+0,0044 |
|
7. |
0,7 |
0,49 |
2,0266 |
|
2,0299 |
+0,0033 |
|
8. |
0,8 |
0,64 |
1,9594 |
|
1,9593 |
-0,0001 |
|
9. |
0,9 |
0,81 |
1,8759 |
1,8735 |
-0,0024 |
|
|
10. |
1,0 |
1,00 |
1,7723 |
1,7723 |
0,000 |
Система относительно А0, А1, А2 имеет в этом случае вид
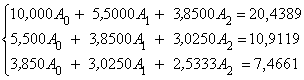 .
.
Решая ее, находим:
А0 = 2,0952, А1 = 0,4423, А2 = –0,7652.
Уравнение параболы имеет вид
у = 2,09552 + 0,4433х – 0,7652х2.
Для сравнения с экспериментальными данными график параболы также изображен на рис. 1.5.
В предпоследнем столбце табл. 1.1 записаны значения функции у, вычисленные по формуле, а в последнем – абсолютные погрешности (разность между полученными результатами и экспериментальными данными).
В случае линейной зависимости, т.е. если мы будем искать функцию вида у = А0 + А1х, то система для нахождения коэффициентов значительно упрощается и принимает следующий вид
 .
.
Эта система называется нормальной системой метода наименьших квадратов
Пример 1.26. В результате эксперимента получены пять значений искомой функции
|
х |
–2 |
0 |
1 |
2 |
4 |
|
у |
0,5 |
1 |
1,5 |
2 |
3 |
Найти функциональную зависимость вида у = А0 + А1х.
Решение. При составлении нормальной системы вычисляем
![]() =16,5;
=16,5; ![]() = 25;
= 25; ![]() =5;
=5; ![]() = 8.
= 8.
Система для определения коэффициентов примет вид:
![]() ,
,
отсюда А0 = 1,175, А1 = 0,425.
Следовательно,
у = 0,425х + 1,175 — уравнение искомой прямой.
Графическая интерпретация приведена на рис. 1.6.
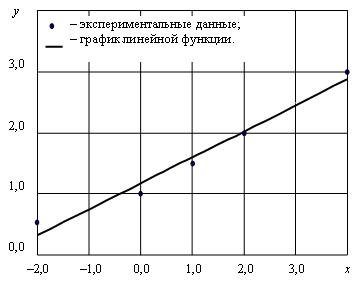
Рис. 1.6. Иллюстрация метода наименьших квадратов первого порядка