Определение. Если функция f(x) определена на отрезке [a, b], непрерывна в каждой точке интервала (a, b), в точке a непрерывна справа, в точке b непрерывна слева, то говорят, что функция f(x) непрерывна на отрезке [a, b].

Другими словами, функция f(x) непрерывна на отрезке [a, b], если выполнены три условия:

1) "x₀Î(a, b): f(x) = f(x₀);

2) f(x) = f(a);

3) f(x) = f(b).

Для функций, непрерывных на отрезке, рассмотрим некоторые свойства, которые сформулируем в виде следующих теорем, не проводя доказательств.

Теорема 1. Если функция f(x) непрерывна на отрезке [a, b], то она достигает на этом отрезке своего наименьшего и своего наибольшего значения.

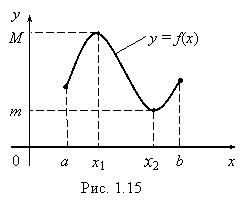
Эта теорема утверждает (рис. 1.15), что на отрезке [a, b] найдется такая точка x₁, что f(x₁) £ f(x) для любых x из [a, b] и что найдется точка x₂ (x₂Î[a, b]) такая, что "xÎ[a, b] (f(x₂) ³  f(x)).

Значение f(x₁) является наибольшим для данной функции на [a, b], а f(x₂) – наименьшим. Обозначим: f(x₁) = M,   f(x₂) = m.   Так как для f(x) выполняется неравенство: "xÎ[a, b] m £ f(x) £ M, то получаем следующее следствие из теоремы 1.

Следствие. Если функция f(x) непрерывна на отрезке, то она ограничена на этом отрезке.

Теорема 2. Если функция f(x) непрерывна на отрезке [a,b] и на концах отрезка принимает значения разных знаков, то найдется такая внутренняя точка x₀ отрезка [a, b], в которой функция обращается в 0, т.е. $x₀ Î (a, b) (f(x₀) = 0).

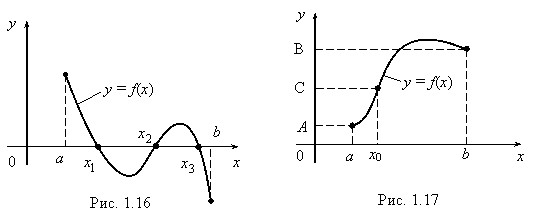
Эта теорема утверждает, что график функции y = f(x), непрерывной на отрезке [a, b], пересекает ось Ox хотя бы один раз, если значения f(a) и f(b) имеют противоположные знаки. Так, (рис. 1.16)  f(a) > 0,   f(b) < 0 и функция f(x) обращается в 0 в точках x₁, x₂, x₃.

Теорема 3. Пусть функция f(x) непрерывна на отрезке [a, b],  f(a) = A,  f(b) = B и A ¹ B. (рис. 1.17). Тогда для любого числа C, заключенного между числами A и B, найдется такая внутренняя точка x₀ отрезка [a, b], что f(x₀) = C.

Следствие. Если функция f(x) непрерывна на отрезке [a, b], m – наименьшее значение f(x), M – наибольшее значение функции f(x) на отрезке [a, b], то функция принимает (хотя бы один раз) любое значение m, заключенное между m и M, а потому отрезок [m, M] является множеством всех значений функции f(x) на отрезке [a, b].

Заметим, что если функция непрерывна на интервале (a, b) или имеет на отрезке [a, b] точки разрыва, то теоремы 1, 2, 3 для такой функции перестают быть верными.

В заключение рассмотрим теорему о существовании обратной функции. Напомним, что под промежутком понимается отрезок либо интервал, либо полуинтервал конечный или бесконечный.

Теорема 4. Пусть f(x) непрерывна на промежутке X, возрастает (или убывает) на X и имеет множеством значений промежуток Y. Тогда для функции y = f(x) существует обратная функция x = j(y), определенная на промежутке Y, непрерывная и возрастающая (или убывающая) на Y с множеством значений X.

Замечание. Пусть функция x = j(y) является обратной для функции f(x). Так как обычно аргумент обозначают через x, а функцию через y, то запишем обратную функцию в виде y = j(x).

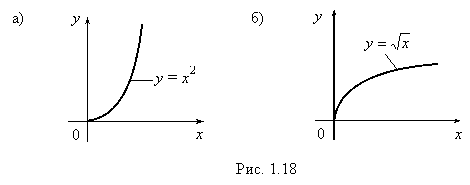
Пример 1. Функция y = x² (рис. 1.8, а) на множестве X = [0, +¥) непрерывна, возрастает и имеет множеством значений Y = [0, +¥). Функция y = x² имеет обратную функцию x =  (рис. 1.8, б), а после переобозначения переменных y = , определенную, непрерывную и возрастающую на X.

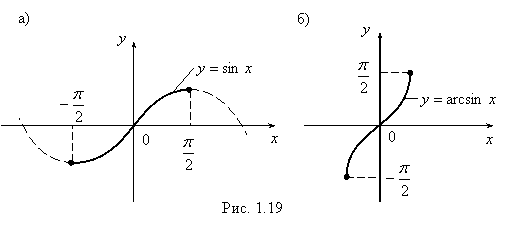
Пример 2. Функция y = sinx (рис. 1.19, а) непрерывна, возрастает на отрезке [–, ] и имеет множеством значений отрезок [–1, 1], поэтому она имеет обратную функцию y = arcsinx (рис. 1.19, б), определенную, непрерывную и возрастающую на отрезке [–1, 1] и имеющую множество значений [–, ].

Заметим, что графики взаимно обратных функций симметричны относительно прямой y = x. Предлагаем построить графики взаимно обратных функций:

1) y = cosx, y = arccosx;

2) y = tgx, y = arctgx;

3) y = ctgx, y = arcctgx;

4) y = e^x, y = lnx.